1 线性方程组
1.1 基本概念
线性方程(Linear Equation)
A linear equation in the variables \(x_1, \cdots , x_n\) is an equation that can be written in the form: \[ a_1x_1 + a_2x_2 + \cdots + a_nx_n = b \]线性方程组(System of Linear Equations/Linear System)
A system of linear equations (or a linear system) is a collection of one or more linear equations involving the same variables解(Solution):
A solution of the system is a list \((s_1, s_2, \dots, s_n)\) of numbers that makes each equation a true statement when the values \((s_1, s_2, \dots, s_n)\) are substituted for \((x_1, x_2, \dots, x_n)\),respectively.解集(Solution Set)
The set of all possible solutions is called the solution set of the linear system线性方程组的等价
Two linear systems are called equivalent if they have the same solution set.
That is, each solution of the first system is a solution of the second system, and each solution of the second system is a solution of the first.
线性方程组的解有三种情况:
- 无解
- 有唯一解
- 有无穷多种解
我们会在 1.2 节中来证明这一点。
- 若线性方程组无解,则称之为相容的(Consisitent)
- 若线性方程组有解(唯一或者无穷),则称之为不相容的(Inconsistent)
1.2 矩阵记号
The essential information of a linear system can be recorded compactly in a rectangular array called a matrix.
例如对于一个Linear System:
\[ \left\{ \begin{aligned} && x_1 - 2x_2 + x_3 & = 0\\ && 2x_2 - 8x_3 & = 8\\ && -4x_1 + 5x_2 + 9x_3 & = -9 \end{aligned} \right. \tag{1} \]
有两种表示方式:
- 系数矩阵(Coefficient Matrix) \[ \left[ \begin{array}{rrr} 1 & -2 & 1 \\ 0 & 2 & -8 \\ -4 & 5 & 9 \end{array} \right] \tag{2} \]
- 增广矩阵(Augmented Matrix) \[ \left[ \begin{array}{rrrr} 1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8 \\ -4 & 5 & 9 & -9 \end{array} \right] \tag{3} \]
一般描述一个矩阵的大小时,使用行列来表述。如果矩阵有 \(m\) 行 \(n\) 列,就表示为 \(m \times n\),读作 "m-by-n matrix" 。
1.3 求解线性方程组(简写做LS)
求解 Linear System 的基本思路就是用一个等价但是又容易求解的 LS 来替换原来的 LS ,然后在求解新的 LS。
基本的方法是消元法。
例1
求解线性方程组\(\pod 1\)
\[ \begin{aligned} &&x_{1}-2 x_{2}+x_{3}=& 0 \\ &&2x_{2}-8 x_{3}=& 8 \\ &&-4 x_{1}+5 x_{2}+9 x_{3}=&-9 \end{aligned} %\quad是空格 \quad \left[ \begin{array}{rrrr} {1} & {-2} & {1} & {0} \\ {0} & {2} & {-8} & {8} \\ {-4} & {5} & {9} & {-9} \end{array} \right] \]
- Step1
\[ \begin{aligned} 4 \cdot \text{[equation 1]}\\ + \text{[equation 3]}\\ \hline \text{[new equation 3]} \end{aligned} \quad \begin{array}{r} 4x_{1}-8 x_{2}+4x_{3} = &0 \\ -4 x_{1}+5 x_{2}+9 x_{3} = &-9\\ \hline -3x_2 + 13x_3 = &-9 \end{array} \\ \Downarrow{经过变换} \\ \begin{aligned} x_{1} - 2x_{2} + x_{3}=& 0 \\ 2x_{2} - 8x_{3}=& 8 \\ -3x_{2} + 13x_{3}=&-9 \end{aligned} %\quad是空格 \quad \left[ \begin{array}{rrrr} {1} & {-2} & {1} & {0} \\ {0} & {2} & {-8} & {8} \\ {0} & {-3} & {13} & {-9} \end{array} \right] \]
- Step2
\[ \begin{aligned} x_{1} - 2x_{2} + x_{3}=& 0 \\ x_{2} - 4x_{3}=& 4 \\ -3x_{2} + 13x_{3}=&-9 \end{aligned} \quad \left[ \begin{array}{rrrr} {1} & {-2} & {1} & {0} \\ {0} & {1} & {-4} & {4} \\ {0} & {-3} & {13} & {-9} \end{array} \right] \]
- Step3
\[ \begin{aligned} 3 \cdot \text{[equation 2]}\\ + \text{[equation 3]}\\ \hline \text{[new equation 3]} \end{aligned} \quad \begin{array}{rr} 3x_{2} - 12x_{3} = &12 \\ -3x_{2} + 13x_{3} = &-9\\ \hline x_3 = & 3 \end{array} \\ \Downarrow{经过变换} \\ \begin{aligned} x_{1} - 2x_{2} + x_{3}=& 0 \\ x_{2} - 4x_{3}=& 4 \\ x_{3}=&3 \end{aligned} \quad \left[ \begin{array}{rrrr} {1} & {-2} & {1} & {0} \\ {0} & {1} & {-4} & {4} \\ {0} & {0} & {1} & {3} \end{array} \right] \]
- Step4 类似的手段,从下往上一次消元
\[ \begin{aligned} x_{1} - 2x_{2} + x_{3}=& 0 \\ x_{2} - 4x_{3}=& 4 \\ x_{3}=&3 \end{aligned} \quad \left[ \begin{array}{rrrr} {1} & {-2} & {1} & {0} \\ {0} & {1} & {-4} & {4} \\ {0} & {0} & {1} & {3} \end{array} \right] \\ \Downarrow{消去1, 2中的x_3} \\ \begin{aligned} x_{1}-2 x_{2} &=-3\\ x_{2} &=16\\ x_{3} &=3 \end{aligned} \quad \left[ \begin{array}{rrrr} {1} & {-2} & {0} & {-3} \\ {0} & {1} & {0} & {16} \\ {0} & {0} & {1} & {3} \end{array} \right] \\ \Downarrow{消去1中的x_2} \\ \left\{ \begin{aligned} x_{1} &=29\\ x_{2} &=16\\ x_{3} &=3 \end{aligned} \right. \quad \left[ \begin{array}{cccc} {1}& {0} & {0} & {29} \\ {0} & {1} & {0} & {16} \\ {0} & {0} & {1} & {3} \end{array} \right] \]
最后求得,方程的解为 \(\pod{29, 16, 3}\) ,如图所示:
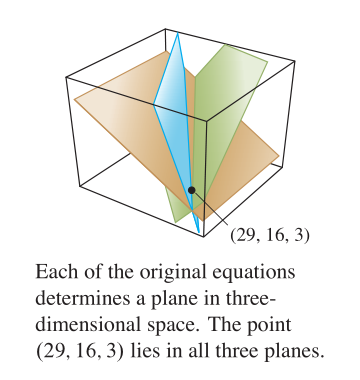
针对例一的说明
例一中的例子充分说明了对线性方程的变换对应与对增广矩阵的行变换。
初等行变换(Elementary Row Operations)
- 倍加变换
- 对调变换
- 倍乘变换
行变换可以实施到任何矩阵中。如果矩阵 A 经过一系列初等行变换可以变成矩阵 B,则称 A 和 B 行等价。
由此可以退出结论:
若两个 LS 的增广矩阵是行等价的,则它们具有相同的解集
1.4 存在与唯一性问题(Existence and Uniqueness)
之前说过,一个方程组的解集可能有三种情况,为了研究这一问题,我们需要提出两个基本的问题:
- 方程组是否相容?
- 方程组若有解,那解是否唯一?
这两个问题会贯穿整个线性代数课程。在本节和下节,我们将会说明如何通过行变换来回答这个问题。
例1
下列方程组是否有解?
\[ \left\{ \begin{aligned} x_1 - 2x_2 + x_3 = 0\\ 2x_2 - 8x_3 = 8\\ -4x_1 + 5x_2 + 9x_3 = -9 \end{aligned} \right. \] 经过行变换,可得增广矩阵的等价形式: \[ \left[ \begin{array}{rrr} 1 & -2 & 1 & 0\\ 0 & 1 & -4 & 4\\ 0 & 0 & 1 & 3 \end{array} \right] \] 可以看出有唯一解。
例2
\[ \left\{ \begin{aligned} x_{2}-4 x_{3} &=8 \\ 2 x_{1}-3 x_{2}+2 x_{3} &=1 \\ 5 x_{1}-8 x_{2}+7 x_{3} &=1 \end{aligned} \right. \]
变换得到: \[ \left[ \begin{array}{rrrr}{2} & {-3} & {2} & {1} \\ {0} & {1} & {-4} & {8} \\ {0} & {0} & {0} & {5 / 2}\end{array}\right] \]
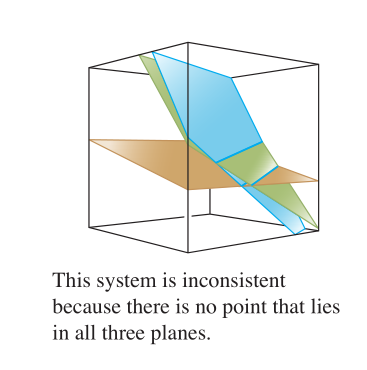
显然无解。我们不妨看一看图,就可以知道,无解的原因是没有点同时落在三个平面上: