这一节介绍基于比较的排序剩下的几个,剩下几个的算法效率都高于前面几个,除了希尔排序之外都是 \(O(n\log{n})\) 级别的。
1. 希尔排序
1.1 思路
插入排序的算法复杂度为 \(O(n^{2})\),但如果序列为正序可提高到 \(O(n)\),而且直接插入排序算法比较简单,希尔排序利用这两点得到了一种改进后的插入排序。
希尔排序在数组中采用跳跃式分组的策略,通过某个增量将数组元素划分为若干组,然后分组进行插入排序,随后逐步缩小增量,继续按组进行插入排序操作,直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序,小的基本在前,大的基本在后。然后缩小增量,到增量为1时,其实多数情况下只需微调即可,不会涉及过多的数据移动。
在每趟的排序过程都有一个增量,至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序);根据增量序列的选取其时间复杂度也会有变化。
1.2 演示
例一
- step1

- step2
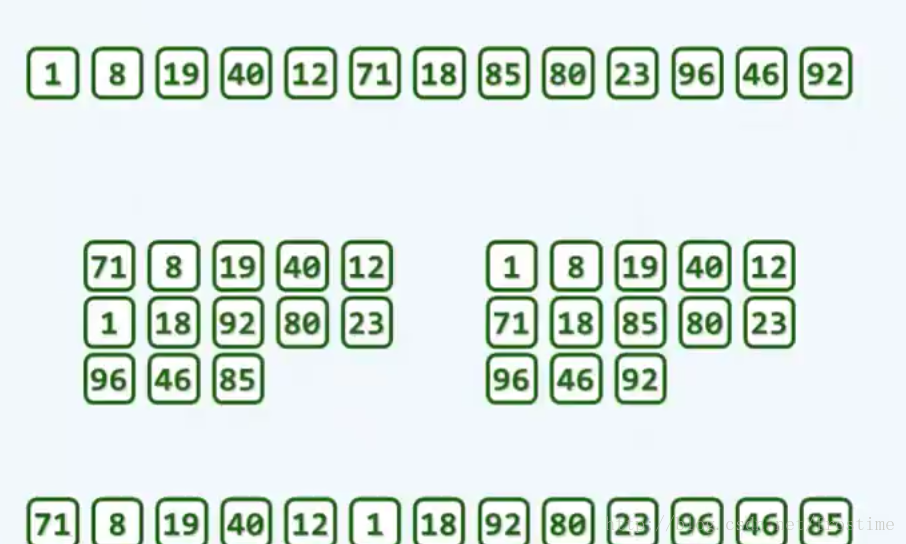
- step3
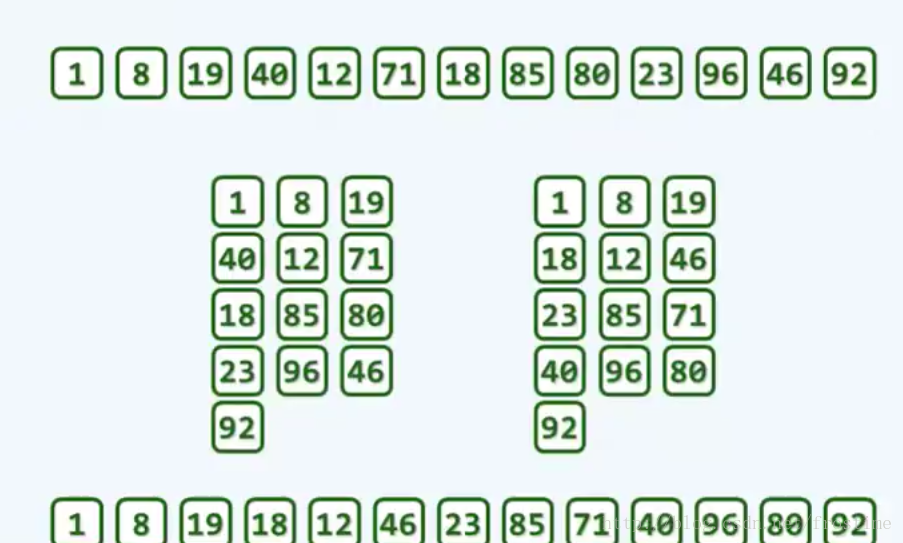
- step4
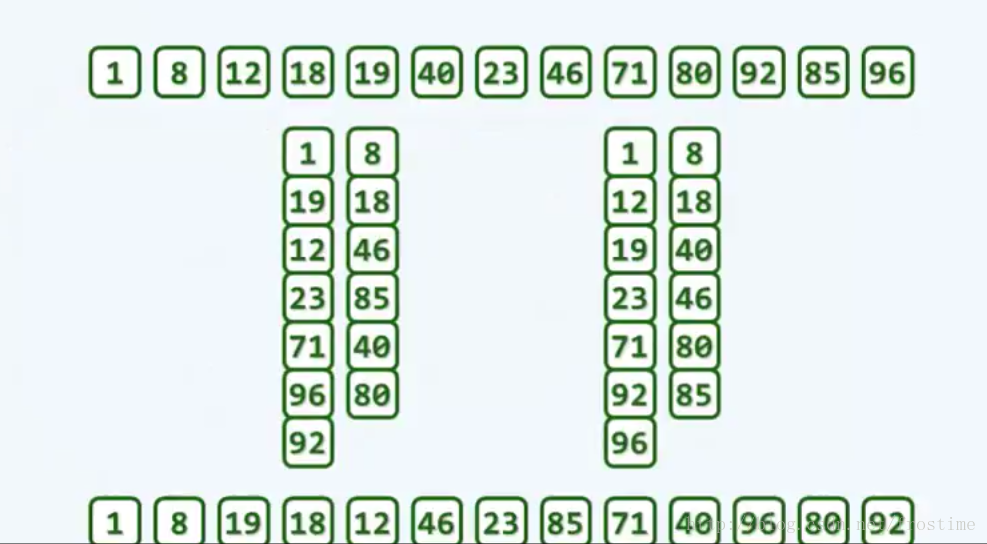
例二
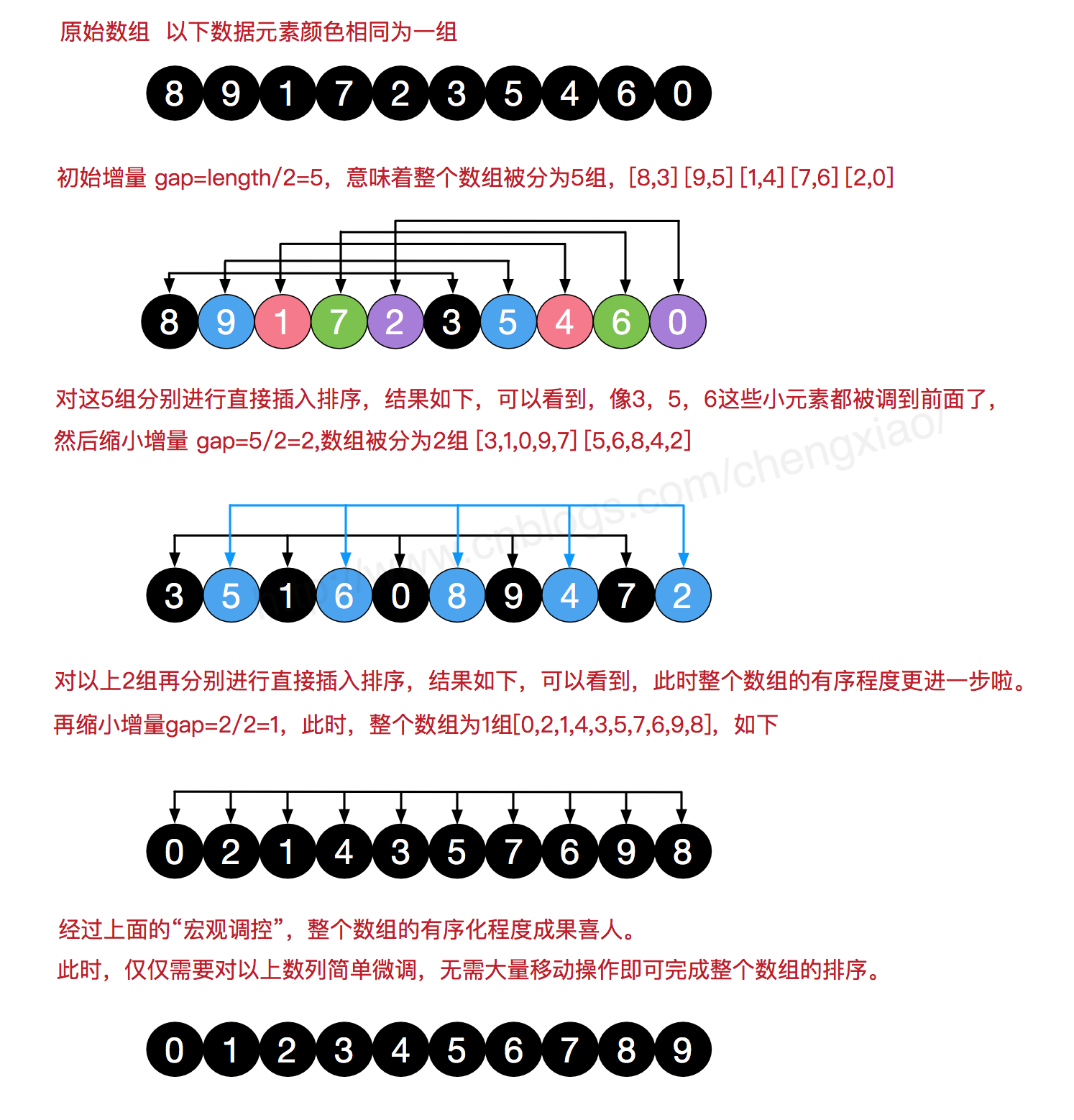
1.3 实现要点
子序列排序方法
希尔排序的一个重要性质是,随着排序次数增长,之前的排序成果会保留下来,整个序列的逆序数会不断减少。
又因为,插入排序的运行时间正比于逆序数,所以我们选择它作为底层排序算法。这样算法的整体运行效率会越来越高。
详细分析,见数据结构mooc
增量(步长)取法
对于步长取法,唯一的要求就是最后一步必须为1,不同的取法对于算法效率的影响很大。
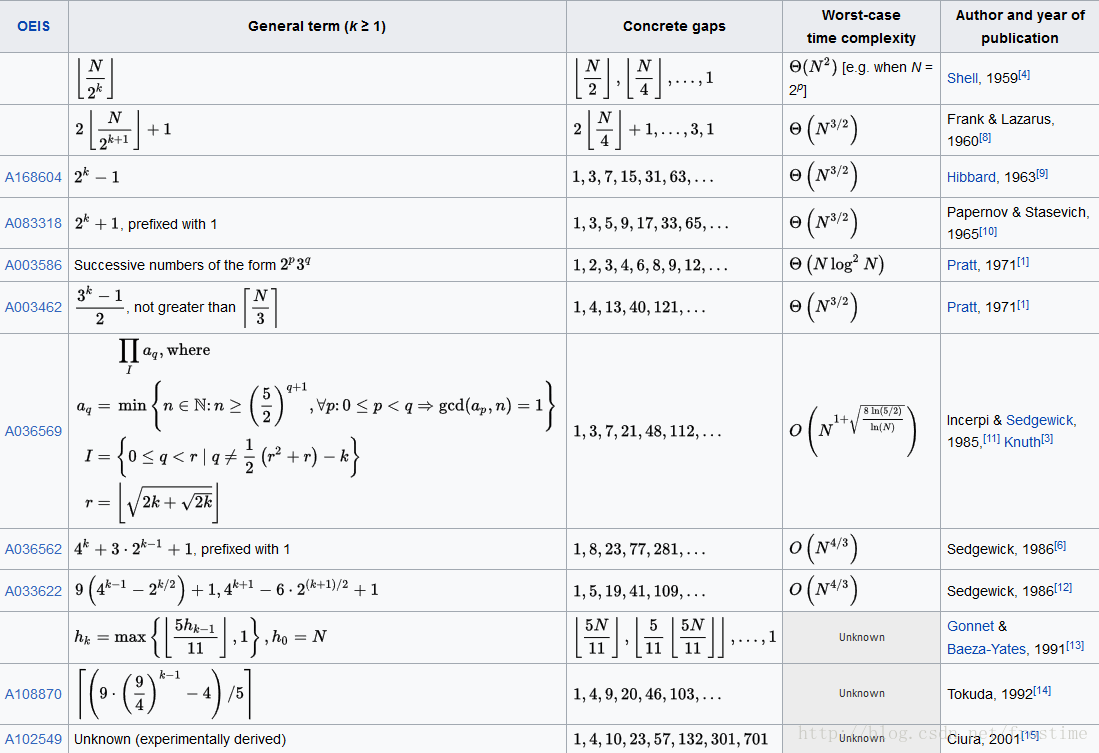
1.4 实现
希尔排序虽然复杂,但实现起来很简单,准确来讲把直接插入算法加个外壳,再把 1 改成 gap 就成了希尔排序。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19/**
* 希尔排序
* 使用 2^n 作为增量,初始为 len / 2,反复整除最后一定可以为1
* 仔细观察发现,一下代码其实就是把插入排序中的 1 改成 gap
*/
void ShellSort(int arr[], int len)
{
for (int gap = len / 2; gap > 0; gap /= 2)
{
//这里基本和插入排序一样了,只是把 1 改成了 gap 而已
for (int i = gap; i < len; ++i)
{
int v = arr[i], j;
for (j = i; j >= gap && arr[j - gap] > v; j -= gap)
arr[j] = arr[j - gap];
arr[j] = v;
}
}
}
这个算法可能有点迷,让人搞不清它在对谁排序,在这里我说明一下。
i
它所定位的是每一个不同的组别,也就是之前图中所看到的矩阵的每一列;而指向了每个组别中的要排序元素,并对其进行相应的操作j
相当于插入排序的j,只不过j的移动是以gap为单位的,因此判断条件中:arr[j - gap] > v
相当于插入排序的arr[j - 1] > vj >= gap
相当于插入排序的j > 0也就是j >= 1
但是在这里,有一个不好看懂的就是该算法的操作并非是一次性将每一组的元素排好序,而是一次只对一组中的一个元素进行排序,然后 i 指针就会移动到下一组,等到 i 移动的次数刚好是j的倍数之后,j 就又会指向之前拍过一次序的组别中的下一个元素并对其排序。
换而言之,该算法的流程是这样的:
graph TD start-->step1 start-->step2 start-->stepx step1-->group1:e1 group1:e1-->group2:e1 group2:e1-->other[...] other[...]-->groupn:e1 step2-->group1:e2 group1:e2-->group2:e2 group2:e2-->other2[...] other2[...]-->groupn:e2 stepx-->other3[...]
而不是
graph TD start-->step1 start-->step2 start-->stepx step1-->group1:e1 group1:e1-->group1:e2 group1:e2-->other[...] other[...]-->group1:en step2-->group2:e1 group2:e1-->group2:e2 group2:e2-->other2[...] other2[...]-->group2:en stepx-->other3[other groups]
虽然以上二者在效果上是等价的,但是前者在操作上要简便一些(虽然理解上难一些)。
2. 归并排序
2.1 思路
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用 分治法(Divide and Conquer) 的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
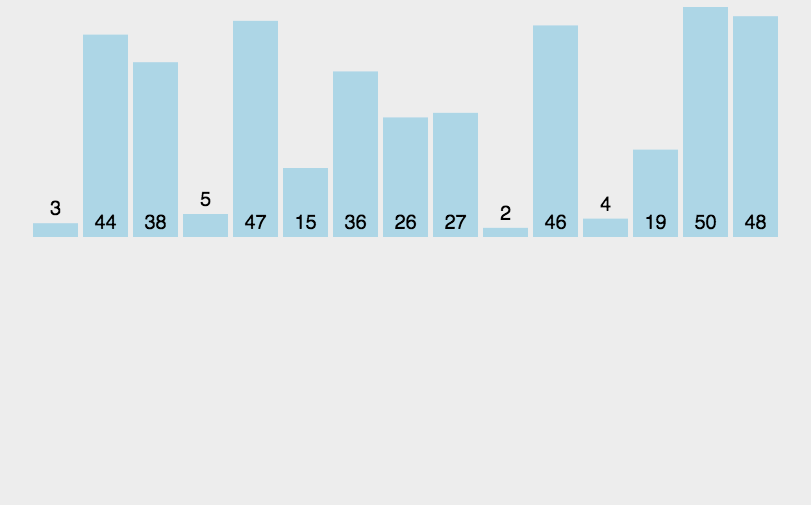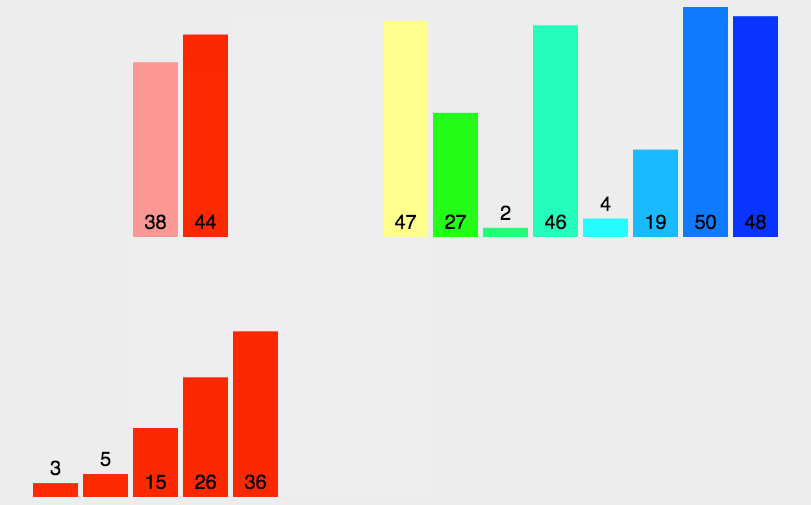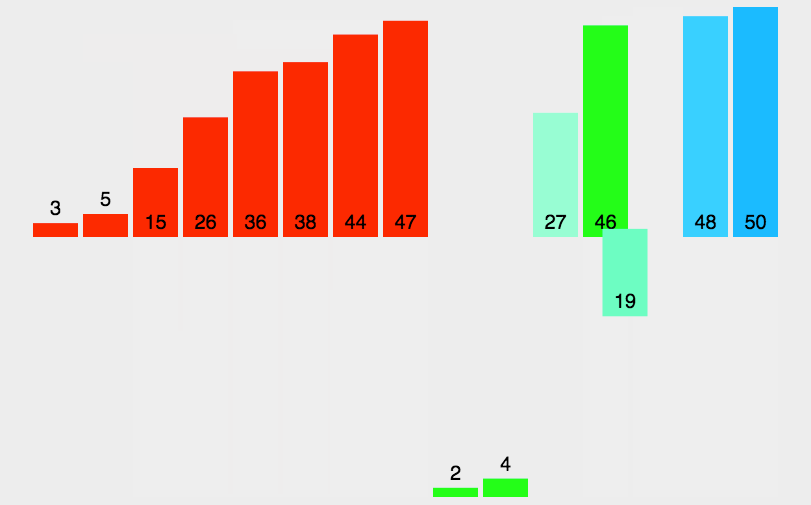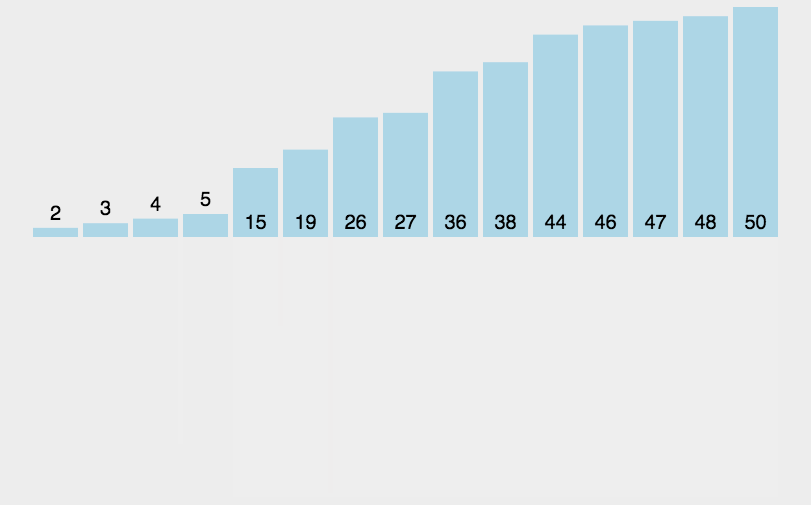
2.2 算法分析
空间复杂度:
归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间:\(n + \log_{}n\);所以空间复杂度为: \(O(n)\)- 时间复杂度
- 最好: \(O(n\log_{}n)\)
- 最坏: \(O(n\log_{}n)\)
- 平均: \(O(n\log_{}n)\)
证明:可知 \(T(n) = 2T(\frac{n}{2} + \Theta(n)\),由主定理可知: \[ n^{\log_{2}2}=n \land f(n) = \Theta(n)\\ \therefore T(n) = O(n\log_{}n) \]
- 稳定性:稳定
2.3 实现
源码
1 | /** |
注意
刚开始的时候我的递归条件是这样的: 1
2
3
4if (beg < end)
{
}
然后我就陷入了死循环出不来了╮(╯▽╰)╭。
问题出在我划分区间的方式,还有结束递归条件的设置上。在这里我的区间设定是[beg, end),这样就会在beg == end时退出递归,想的倒是挺好,不过来看看这种情况:
假设在某次递归中,beg代表了index = 1的元素,相应的end代表index = 2,整个区间只有一个元素。这样mid = 1 + 1 / 2 = 1,然后我们就会发现函数一直朝MergeSort(mid, end);的方向递归下去,无法返回了。
所以为了避免这种情况,请记住:
将递归结束条件设置为区间内只有一个元素或者空表!!!。
记住这一个原则,然后在根据自己的区间设置规范来调整就行了,比如: 1
2
3
4
5
6
7
8
9//显然这里是[first, last]
//当first == last 说明只有一个元素结束递归
if (first < last)
{
int mid = (first + last) / 2;
mergesort(a, first, mid, temp); //左边有序
mergesort(a, mid + 1, last, temp); //右边有序
mergearray(a, first, mid, last, temp); //再将二个有序数列合并
}
3. 快速排序
快速排序使用分治的思想,通过一趟排序将待排序列分割成两部分,其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序,以达到整个序列有序的目的。
3.1 思路
快速排序的原理
假设我们有这样一个序列,它可以分为前后两个子序列,且满足:
\[ max(S_{L}) \leqslant min(S_{R}) \]
这样,如果我们将左右两个序列分别排序(分治的思想),然后将子序列再连接起来,则整个序列一定是有序的。
快速排序正是运用了这一个事实,将整个序列不断分为左小右大的两个子序列递归排序,最终使得整体排序完成。
可以看到,快排与归并有一定相似之处。不同的是,归并的关键在于怎么将子序列合起来,快排的关键在于怎么划分出符合要求的子序列。快排的最大障碍也就在这里。
轴点
为了实现这一想法,我们首先要引入一个概念——轴点(pivot)。
轴点是在序列中满足一种特殊要求的元素:在轴点左侧区间的所有值都小于轴点的值,右侧区间的所有值都大于轴点的值。
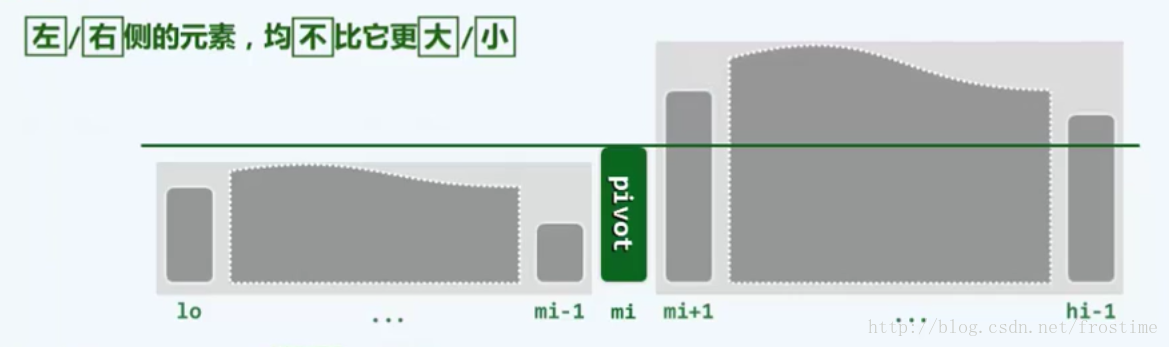
结合以上说明,我们可以得出以下结论:
- 以任意一个轴点为界,整个区间呈现左小右大的状态。将轴点左侧和右侧的序列分别排序,再直接串联起来,就会得到整体有序的序列。(正好满足我们的需求)
- 每一个轴点的位置必然是它在最终有序序列中的位置。换而言之,每一个轴点其自身一定是无须移位的。
- 只要在序列中确定轴点,就可以递归式地解决问题。
1 | Iterator pivot; |
由此我们可以得知,快速排序的核心就是如何找到轴点。
构建轴点
然而一个麻烦的问题在于:在一个序列中很可能根本就没有先天性的轴点。比如任意一个乱序序列,每一个元素都不能作为轴点。
因此,我们需要找到一些候补轴点,通过一系列地处理将它培养成为轴点。上述算法中的Partition方法的作用就是构造一个有效的轴点。
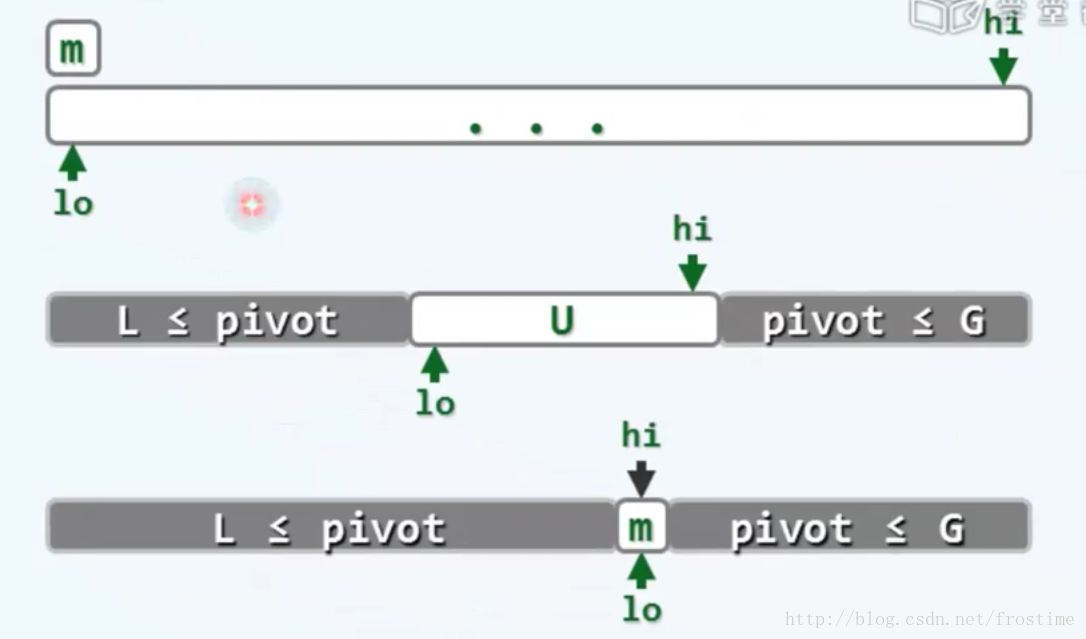
如图所示:
- 用两个指针指向两段
- 不断将元素放入区间U
- 最终将选定的轴点的值放入m处
- 结束算法
演示
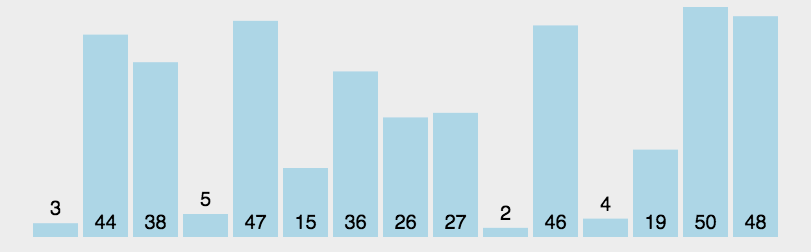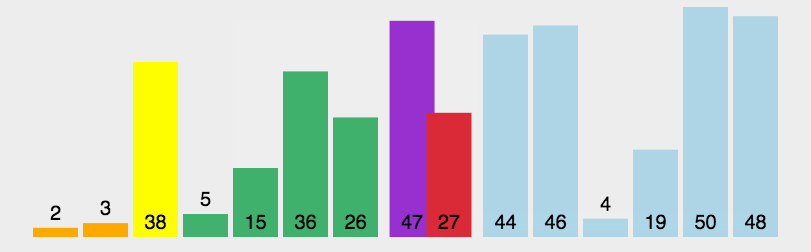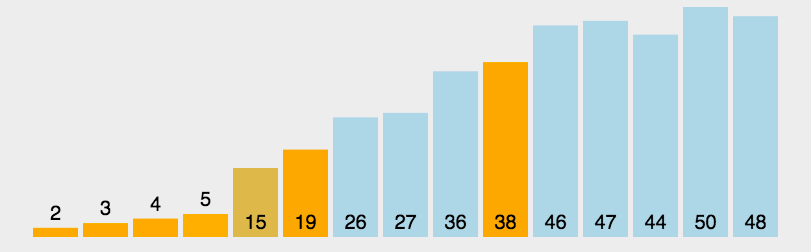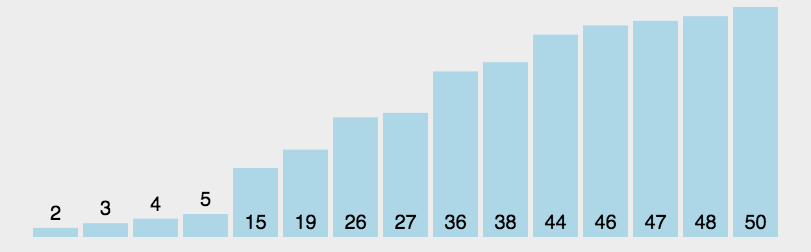
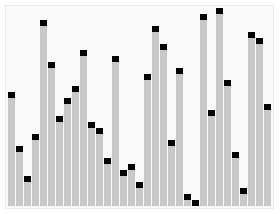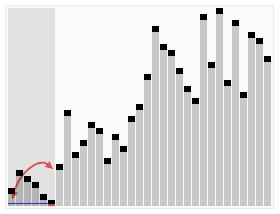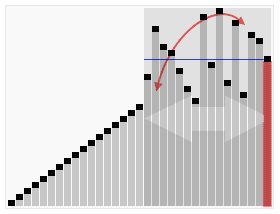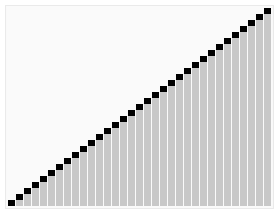
2.2 算法评估
快速排序的实际效率取决于选定轴点的最终位置。轴点越接近中点、划分越平均,则算法效率越高。
- 空间复杂度:
- 时间复杂度:
- 平均:\(O(n\log_{}n)\)
- 最好:每次都划分在中点 \(O(n\log_{}n)\)
- 最坏:每次都划分在最大(最小点) \(O(n^{2})\) (与冒泡排序相当)
- 稳定性:不稳定
- 输入敏感性:
2.3 实现
1 | /** |
附加说明:
注意一下在递归时,与归并算法不同的一点是,这里的
pivot有独特的含义,是已经就位了的轴点元素,因此进行子递归是不应该将它放入递归区间。
应该是这样:
1 | //正确 |
而不是
1 | //错误,不能将pivot也包括进去 |
要是真一个手抖写成了后者,就会陷入无尽的递归而不得脱身╰(‵□′)╯
这里我们将候补轴点的选择统一安排为序列第一个元素,事实上这并不好(就像希尔排序选择2的指数一样不好)。
但是如果我们选取的枢轴不是第一个元素,在执行这个算法中,就会存在第一个元素丢失的风险。因此我们不妨这样做:选取第一,中间,最后的元素中中间者作为枢轴元素,然后将它与第一个元素交换。
4. 堆排序
4.1 思路
堆的性质见其他博文。
思路很简单:
1 | 把 arr[0, end) 建立成一个大顶堆 |
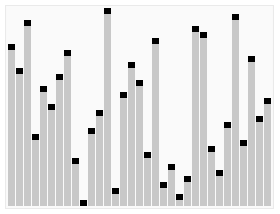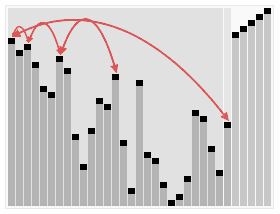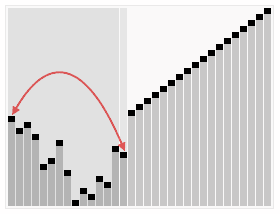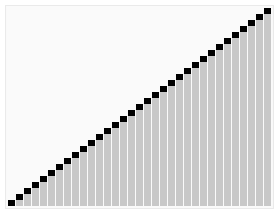
4.2 实现
1 | int Parent(int i) |
4.3 算法评估
- 空间复杂度:\(O(1)\)
- 时间复杂度:
- 平均:\(O(n\log_{}n)\)
- 最好:\(O(n\log_{}n)\)
- 最坏:\(O(n\log_{}n))\)
- 稳定性:不稳定
- 输入敏感性: