1. 素数的性质
1.1 性质一: 分布
\[ \lim_{x\to \infty}\pi(x) = \lim_{x\to \infty}\frac{x}{\ln{x}} \]
其中 \(\pi(x)\) 表示不大于x的所有素数的个数。在 x 比较大时,通常这个误差不超过 15%。
1.2 性质二: 6的倍数
任意大于等于5的素数都与6的倍数相邻
例如: > 23 + 1 = 4 * 6
> 17 + 1 = 3 * 6
> 31 - 1 = 5 * 6
1.3 性质三: 质因数分解
任何一个大于1的自然数都可以分解成几个素数连乘积的形式,而且这种分解是唯一的
1.4 性质四: 梅森数
如果 \(2^{p}-1\) 是素数,那么P一定也是个素数
1.5 性质四:费马小定理
假如 \(a\) 是一个整数, \(p\) 是一个质数,那么 \(a^p - a\)是 \(p\) 的倍数,\(a^p\) 和 \(a\) 对于模 \(p\) 同余。。可以表示为。
\[ a^p \equiv = a\ (mod p) \]
特别的, 如果 a 和 p 互质,这个定理也可以写成: \[ a^{p-1} \equiv = 1\ (mod p) \]
2. 判断质数
判断质数的算法是最古老也是最常用的。
2.1 最简单的方法:试除法
最直观的方法被称为试除法,即给定一个数n,不断的试探从2~n之间的数是否可以整除n。
1 | private static boolean isPrime1(long n) |
不过以上算法也有一些可以改进的地方:
- 我们无须一直试到 \(n\),反之到 \(\sqrt{n}\) 就可以了
- 除了 2 以外,所有可能的质因数都是奇数。所以可以先尝试 2,然后再尝试从 3 开始一直到 \(\sqrt{n}\) 的所有奇数
由此我们可以给出一个基本的解答:
1 | private static boolean isPrime2(long n) |
然而到这里还没完。还记得我们之前提到的素数的性质吗?
任意大于等于5的素数必然邻近于6的倍数
这是一个非常有用的性质,利用它我们可以继续优化我们的算法:
1 | private static boolean isPrime3(long n) |
然而以上的算法还可以简化。这就需要用到我们之前提到的质因数分解的性质了:
大于1的自然数都可以分解成几个素数连乘积
\[ \begin{aligned} & \because \text{n为合数} \Rightarrow \exists x, y(x \leqslant \sqrt{n} \land y \geqslant \sqrt{n} \land x * y = n)\\ & \text{又} \because x \text{可分解为(质数a * 某个数b),且a必然小于等于} \sqrt{n}\\ & \therefore \text{若n为合数} \Rightarrow \text{n必有一个小于等于}\sqrt{n}\text{的质因子a}\\ & \therefore \text{若对于一个数n,}\not\exists x(x \leqslant \sqrt{n} \land \text{x是质数}\land \text{x是n的因子}) \Rightarrow \text{n为质数} \end{aligned} \] 根据以上推理,可以得出结论:
\[ \begin{aligned} & \text{若}\exists S, \forall x(x \leqslant \sqrt{n}\land \text{x是质数} \land x \in S)\\ & \text{且对于}\forall x\in S \text{都有} n\ mod\ x \neq 0\\ & \text{则n必为质数} \end{aligned} \]
好消息是,上面的集合 \(S\) 我们是可以找到的。这个集合S就是从6一直到 \(\sqrt{n}\) 的路上,所有同 \(6k\) 相邻的数。这个集合必然包含了所有的质数和一部分其余的合数。有了以上的数学基础我们就可以写成试除法中(也许是)最高效的算法了:
1 | private static boolean isPrime3(long n) |
3. 质数构造算法(筛法)
很多情况下我们面临着构造质数的需求:
给定一个数n,请求出所有小于n的质数
例如: n = 10,则打印出 2 3 5 7
给定一个数n,请求出前n个质数
例如: n = 10,则打印出 2 3 5 7 11 13 17 19 23 29
这时我们会用到一种叫做埃拉托斯特尼(Eratosthenes)筛选法的算法。这个算法的作用是求出0~n之间的所有质数。大体思想如下:
- 构造一个长度为n的序列,代表了从1到n所有的数据
- 因为0,1不是质数,所以我们从2开始,令其为x
- 将所有x的倍数剔除掉
- 将x赋值为大于原x的最小的质数
- 重复步骤3,4
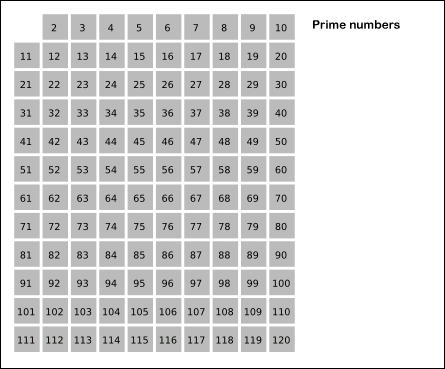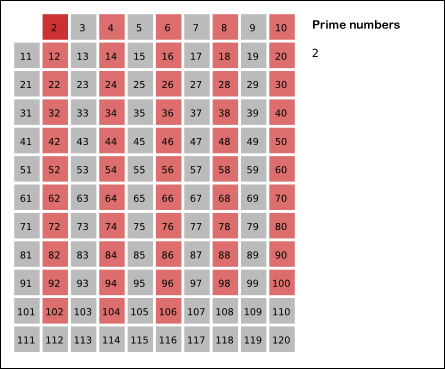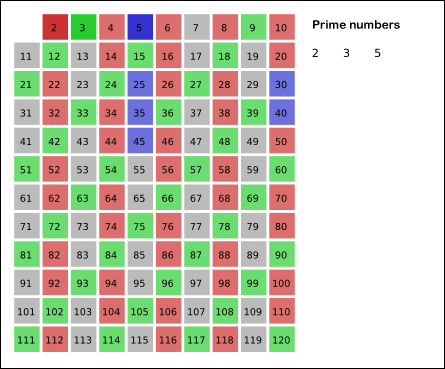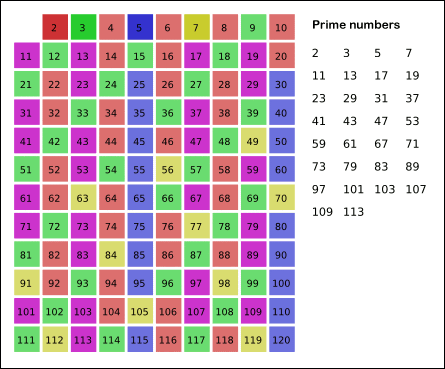
这里有几个问题
怎么找到下一个最小的质数?
其实这个问题很简单。不妨假设a,b分别为相邻两个质数。则由于我们是从前往后不断筛选,则在a处理完了以后,它的下一个未被剔除的元素就是b
这个表要怎么构建?
通常我们是构建一个长度为n的布尔型数组,这样比较节省空间
但是还有一个更节省空间的办法:使用一个长度为n的二进制串
实现如下:
1 | //所有使得isPrime[i]为true的i即为质数 |
有两点需要注意:
j从 \(i ^ 2\) 开始:其实按照我们之前的分析,
j理应从2 * i开始,但是要注意到在迭代到i之前,那些2 * i、3 * i等等都已经被筛选掉了。所以直接从i^2开始即可i一直到sqrt(range)就可以了有了1的基础,不难证明当
i > sqrt(range)时,第二重循环已经是在做无用功了
该算法复杂度为: \(O(n\log{n})\)
4. 求最大质因数
4.1 引论题目
The prime factors of 13195 are 5, 7, 13 and 29.
What is the largest prime factor of the number 600851475143 ?
4.2 一个不好的思路
寻找最大质因数一个最简单的思路如下:
1 | for (long i = n; i >= 2; --i) |
但是在这一题中,情况很特殊,由于n十分大,如果按照上面的方法来时间花费极大。而且我们还不得不额外编写用于判断质数的算法。
可想而知对于n极大的数而言以上算法的效率很低。
4.3 一个更高效的算法
1 | private static long maxPrimeFactor(long n) |
以上算法就是利用短除法求解最大质因数的算法,抛开那个什么短除法不谈,我们仔细现象,就会发现它本质上其实和筛法有异曲同工之妙。通过简单的数学分析我们可以证明它的工作原理和几个特性:
while循环的工作本质上就是在范围n内筛选剔除掉所有i的倍数可以证明每次进入
while循环时,i必然为n的一个质因子可以用反证法证明:
假设当前的
i == y,且y是一个合数,它的上一个质数是x,下一个质数是z,则:n % y == 0- 由合数的分解性质可得,必然存在一个质数
a < y,使得y % a == 0 - 综合1、2两点可得必然存在质数
a < y,使得n % a == 0
- 然而由于在
i == y之前所有的质因子已经被剔除,这就与3产生了矛盾
- 所以原命题为假,
i不可能为合数,必然是n的一个质因子
若n是一个质数:
则可以证明当且仅的
i == n时,才会进入while循环,执行一遍以后算法退出,此时i == n+1,所以只需返回i-1即可若n是一个合数:
由于进入
while循环的i是原始的n从小到大的质因子,因此整个for循环相当于不断在做质因数分解,直到最后一步,退化成了情况3,这时的i就是最大质因数。然而在退出
for循环时,i又会多加一,所以最后要减回来
5. 分解质因数
事实上从我们前面一个算法的分析来看,我们很容易发现,实际上那就是在分解质因数。所以基本上把前面一个算法拷贝过来就行了:
1 | private static void resolvePrimeFactor(long n) |
现在我们来看另一个问题,这个算法的效率怎么样?
实际上,尽管用到了二重循环,然而算法复杂度却甚至小于 \(O(n)\) ,具体而言:
若n是一个质数:
这是最糟糕的情况,算法复杂度为 \(O(n)\)
若n是一个合数:
我们注意到
n在这个过程中是不断被缩小的,且while循环执行的次数恰好等于n的质因子数目。这种情况下就要取决于n本身的性质了。最好的情况下,n是一个2的幂,这时算法的复杂度直接降到了 \(O(\log{n})\) 。
对于一般情况下,可能要取决于n的最大质因子
k,可以发现这种情况下,复杂度因为 \(o(k)\) ,考虑到一般k << n,这也是可以接受的
5.1 质因数的个数及其优化版
1 | int n = 0; |
再进一步优化
1 | int n = 0; |