1. 概论

二叉搜索树（Binary Search Tree, BST），（又：二叉查找树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
它的左、右子树也分别为二叉排序树

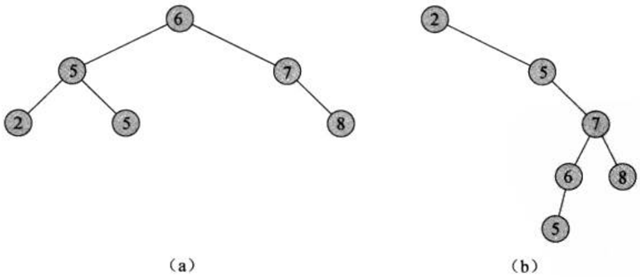
顾名思义，BST常用于搜索结构。现在我们给出通常对BST进行的操作的概述：

插入一个特定值的结点
删除一个特定值的结点
判断一个给定值是否存在
找出最大/最小值
遍历打印整棵树
清空

由于树的递归定义，我们一般使用递归算法来完成操作。因为BST的平均搜索深度为 \(O(\log_{}{n})\) 所以无序担心栈溢出。

下面给出BST实现的类模板接口。

template<typename T>
class BinarySearchTree
{
public:
    enum Traversal{preorder, inorder, postorder};
    struct BinNode
    {
        T val;
        BinNode *left;
        BinNode *right;
        BinNode(T v, BinNode *l = nullptr, BinNode *r = nullptr) : 
                val(v), left(l), right(r) {}
    };
public:
    BinarySearchTree();
    BinarySearchTree(const BinarySearchTree &other);
    ~BinarySearchTree();
    const BinarySearchTree & operator=(const BinarySearchTree &other); 
    
    //Manipulation
    void insert(const T &val);
    void remove(const T &val);
    void makeEmpty();
    
    //Info
    const T& findMin() const;
    const T& findMax() const;
    BinNode* contains(const T &elem);
    void print(Traversal order) const;
    bool empty() const;
private:
    BinNode * findMin(BinNode *cur) const;
    BinNode * findMax(BinNode *cur) const;
    //由于不改变指针指向，不需要使用指针的引用
    BinNode* contains(const T &elem, BinNode *cur);
    
    //由于一开始root为nullptr，要想在程序中更改其指向，就要写作指针的引用
    void insert(const T &val, BinNode *&cur);
    void remove(const T &val, BinNode *&cur);
    void makeEmpty(BinarySearchTree *& root);
    
    void preorderPrint(BinNode *root) const;
    void inorderPrint(BinNode *root) const;
    void postorderPrint(BinNode *root) const;
private:
    BinNode *root;
};

在这里还有一些疑问，我们先做简单解释：

程序中在 public 和 private 中分别出现重载的函数是为了方便使用递归。public 中的方法提供对外接口并隐藏关键信息；private 中的方法用于实现递归算法。
之所以有些参数类型为 *& 是因为在执行过程中传入的指针指向需要改变。

此外需要注意的是，在这里数据类型 T 必须已实现了 operator <。如果没有实现重载的话也可以使用一个函数对象:

template<typename T, typename Comparator = less<T>>
class BinarySearchTree
{
    Comparator lessThan;
};

其中 less 是定义在标准库 <functional> 中的一个函数类模板。使用时可以:

1	if (lessThan(x, cur->val);)

2. `contain`

contain 方法主要用于判断元素是否存在于BST当中。

bool contains(const T &elem) const
{
    return contains(elem, root) != nullptr;
}
BinNode * contains(const T &elem, BinNode *cur) const
{
    if (cur == nullptr)
        return cur;
    else if (elem < cur->val)
        return contains(elem, cur->left);
    else if (cur->val < elem)
        return contains(elem, cur->right);
    else
        return cur;
}

算法的思想很简单：如果根节点就是，那就返回根节点；否则，可以利用BST的性质判断目标结点所在的位置，然后递归处理。该算法有几点要注意的：

T 需要对 < 进行重载
对根节点是否为空的判断必须放在最前面
把最不可能发生的情况放在最后面判断
指针无需以引用的方式传递
两个方法的返回值不同，是因为外部不需要关系该值的具体位置(信息隐藏)，而内部则不然。

算法评估:

时间	空间
\(O(\log_{}{n})\)	\(O(\log_{}{n})\)

可以看出这个递归算法本质上是一个尾递归。不过由于对栈的使用最多不过 \(O(\log_{}{n})\) ，所以这里的尾递归是安全合理的。
同时完全可以写成非递归算法:

BinNode * contains(const T &elem) const
{
    BinNode *cur = root;
    while (cur != nullptr)
    {
        if (elem < cur->val)
            cur = cur->left;
        else if (cur->val < elem)
            cur = cur->right;
        else if (elem == cur->val)
            return cur;
    }
    return nullptr;
}

可以看到，非递归算法的形式也十分简单。不过注意的是即使写成非递归算法，也不应该舍弃对外接口，因为 BinNode* 不是外界应该能获得的，出于信息隐藏的考虑，对外接口仍应该是:

1	bool contains(const T &elem) const;

3. `findMax` 和 `finMin`

在BST中，查找最大最小值是极为简单的:最小值在最左边；最大值在最右边。原理很简单，仔细考虑一下BST的性质就能想明白。

const T & findMin() const
{
    return findMin(root)->val;
}
const T& findMax() const
{
    return findMax(root)->val;
}

以上两个算法提供对外接口。而内部则由另一个算法完成:

BinNode * findMin(BinNode *cur) const
{
    if (cur == nullptr)
            return nullptr;
    if (cur->left == nullptr)
        return cur;
    return findMin(cur->left);
}

再次强调一下，对空指针的检查一定要放在最前面。同时，由于我们是pass-by-value，因此对指针的变更不会有问题。

注意，这里我们的返回值类型为BinNode*，而对外接口的返回值则为const T &。这是因为我们不希望外界可以获取直接访问结点的权限，而内部的方法却又有这样一个需求。

顺便还有一点，最好不要写成这样:

if (cur == nullptr)
    return nullptr;
if (cur->left != nullptr)
    return findMin(cur->left);
return cur;

这里我们使用了尾递归，希望编译器能对其优化。如果写成后者就不是尾递归的形式了。

事实上，既然可以使用尾递归，就说明一定可以更改为迭代的形式。事实上在这里，我们更支持使用迭代而非递归。

//本迭代式十分简单，总体而言更优于使用递归
BinNode * findMax(BinNode *cur) const
{
    if (cur != nullptr)
        while (cur->right != nullptr)
            cur = cur->right;
    return cur;
}

4. `insert`

4.1 基本说明

如果你仔细观察对外接口的参数列表你会发现它只指定了值，而不指定位置；同时也没有返回值。这和我们在单链表中的做法大不相同。

//在单链表中，这个接口往往定义为
//iterator insert(const T &val, const iterator &pos);
void insert(const T &val)
{
    insert(val, root);
}

而这就反映了BST的不同之处，具体而言：

我们在链表中指定位置是因为链表对元素的位置没有要求。而在BST中，元素的位置必须严格遵守规定，不可由用户指定。而事实上，在BST中添加元素往往意味着建立一个新的叶子节点。
我们设置一个返回迭代器的方法是为了便于连续插入以及修改元素。这两点在BST中都毫无用处:
- 大部分情况下插入的元素的位置基本都隔得很远
- 我们一般把BST当作集合来使用，不允许修改其中的元素

4.2 算法思路

若在BST中建立新结点，则它必为叶节点。
插入和查找思路类似，首先查找有没有和给定值相同的，如果有进行相应处理(注意，有多种处理方式)；如果没有找到，那么创建新的节点。并更新每个节点的值。

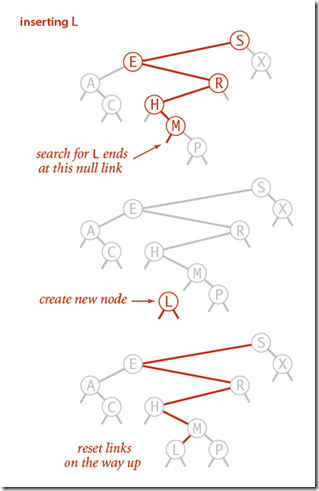
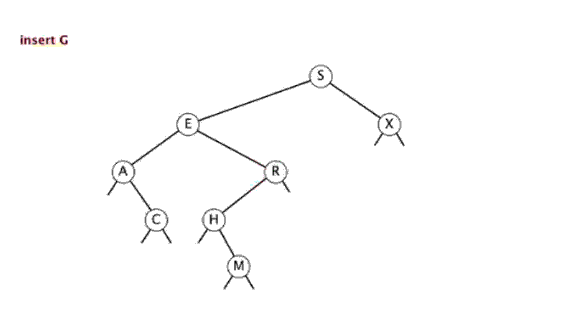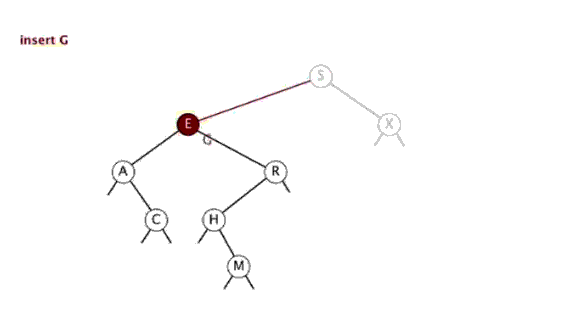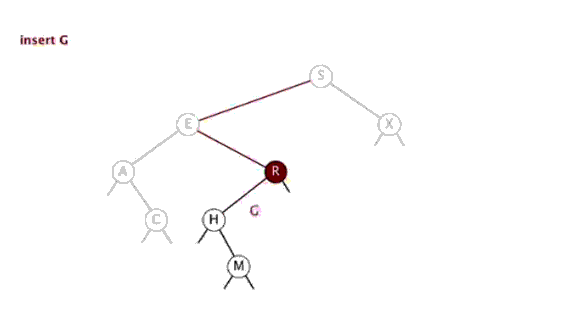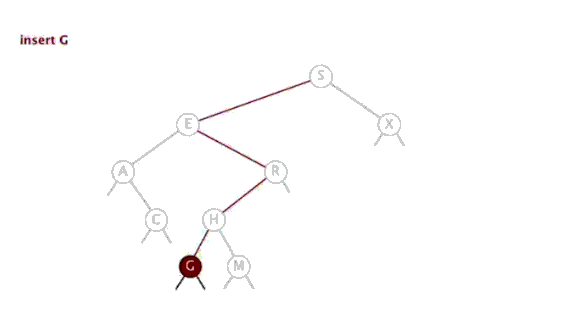
4.3 实现

4.3.1 递归版

使用引用

void insert(const T &val)
{
    insert(val, root);
}
void insert(const T &val, BinNode *&cur)
{
    if (cur == nullptr)
    {
        //相当于root->left = new BinNode()（或是right）
        cur = new BinNode(val);
    }
    else if (cur->val < val)
    {
        insert(val, cur->right);
    }
    else if (val < cur->val)
    {
        insert(val, cur->left);
    }
    else 
        ;//重复元素，我们什么都不做
}

老生常谈的，对nullptr的处理我们必须要放在最前面。不同之处在于这次是要创建一个结点，让传入的cur指向它以此在BST上连上一个新结点。

问题来了，为什么参数名为 BinNode *&cur ？这是因为在 cur = new BinNode(val); 这一句中 cur 的指向被改变了，如果不使用引用，就无法将新结点连入。

使用了引用之后，如果称前一次递归调用的指针 cur 为 p，那么在本次方法中，cur 就相当于 p->left (或 p->right )。下图为模拟在递归中 cur 的含义:

graph TD
a(root)-->b(root->left)
b(root->left)-->c(root->left->right)
c-->d(...)

最终 cur = new BinNode(val); 就相当于 root->left->right->...->left = new BinNode(val);。这样结点就链接上去了。

不使用引用

考虑到很多语言不支持pass-by-reference，我们也给出按值传递的实现。同样，只需要添加一些赋值操作和返回值就行了。首先我们规定 insert 算法返回指向子树的指针，根据这个就可以写出相应算法:

void insert(const T &val)
{
    root = insert(val, root);
}
BinNode * insert(const T &val, BinNode *cur)
{
    //处理子树的根节点，让它连到更新后的子子树上
    if (cur == nullptr)
    {
        cur =  new BinNode(val);
    }
    else if (cur->val < val)
    {
        cur->right = insert(val, cur->right);
    }
    else if (val < cur->val)
    {
        cur->left = insert(val, cur->left);
    }
    else 
        ;//重复元素，我们什么都不做
    //返回子树根节点让它连到父节点的left或right或root上
    return cur;
}

递归逻辑为：cur 是一个子树的根节点，每次只要将元素插入到 cur 的子树中，再返回 cur 将它连到父节点上就可以了。

4.3.2 非递归版

void insert(const T &val)
{
    //处理特殊情况
    if (root == nullptr)
    {
        root = new BinNode(val);
        return;
    }
    
    BinNode *parent = root, *cur = root;
    while (cur != nullptr )
    {
        if (val < cur->val)
        {
            parent = cur;
            cur = cur->left;
        }
        else if (cur->val < val)
        {
            parent = cur;
            cur = cur->right;
        }
        else
            return;//已存在，什么都不做
    }
    (val < parent->val)? 
    parent->left = new BinNode(val): parent->right = new BinNode(val);
}

算法很清楚，首先处理特殊情况空树。然后迭代移动 cur 指针。cur 的作用在于确定是否到了可以插入的位置，真正执行插入的是 parent 指针，因为那时候 cur 已经是 nullptr了。(注意不要漏掉了已存在的情况)

注意不要写出这样的糟糕算法：

void insert(const T &val)
{
    if (contains(val))
    {
        //....
    }
    //....
}

这是我在网上看到的极其糟糕的一个算法， contains 完全是多余的。因为BST的特殊性，insert 的过程本身就在判断存在性，所以不要做无用功。

4.4 对已存在元素的处理进行一个小改进

现在让我们重新来考虑一下之前一直无视的一个问题：如果代插入元素已存在怎么办？

之前我们的做法是像正统的集合一样无视之。但是如果我们想要利用BST来实现一个 multi-set 呢？显然这个问题就不可忽视了。

一个最为直观的做法是如果存在，就再插入一个结点。但这样做一点也不好，问题有两个:

由于插入点必然在已存在结点的子树上，无论是插入在左子树还是右子树上，都破坏了BST的逻辑。
如果程序中有大量插入重复数据操作，BST的高度将会急速增长，这是很致命的！

所以我们的改进做法是在 BinNode 的数据域中增加一项 frequency ，用来记录结点被插入的次数。当重复插入时，只需将 frequency 加一即可。

表面上看这增加了空间消耗，但比起BST的高度增加，区区四分之一的额外空间不足挂齿。

5. `remove`

5.1 基本思路

BST的删除算法会相对困难一些，当然我们这里指的是 frequency == 1 的“真删除”操作。

首先我们先要搞清楚对一个BST进行删除操作意味着什么。

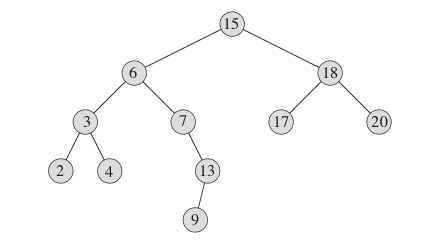
经过仔细分析，我们发现可以将删除结点分为三种情况:

删除一个叶子结点
删除一个只有一个孩子的父节点
删除同时有两个孩子的父节点

在这其中1，2两种情况比较简单。

对于情况1，只需直接删除即可。对于情况2，就完全退化为一个普通单链表删除结点的问题了。大致方式如下:

//注意，要么使用引用，要么待会返回cur给父节点
BinNode *oldNode = cur;
cur = (cur->left != nullptr)? cur->left : cur->right;
delete oldNode;

麻烦在于情况3。

就比如说如果我想删除值为6的结点，该怎么做？更准确的来讲，将结点6删除后，原本结点6的位置该怎么办？显然，不能像在单链表里的那样简单粗暴地让结点的前驱指向其后继。因为作为前驱的父节点只有一个左孩子指针，而他要面对的确是两棵子树。

一般在树中的做法是找一个子树结点让它来代替结点6的位置。在BST中自然也不例外，所以剩下的问题就是找哪个？

不妨做一个简单的分析。目标结点必须满足这样一个条件：

\[ maxValue(leftSubTree) \leqslant value(Node) \leqslant minValue(rightSubTree) \]

继续分析，该结点可能存在的位置无外乎两种：

结点在左子树上
结点在右子树上

不妨假设结点x在右子树上，那么 value(x) 必然满足不等式左侧的关系。显然要想同时满足右侧关系，x必为右子树上的最小值。同样的分析也可适用于左子树。

这样我们就对BST树的删除有了一个基本思路。

需要注意的是删除操作必然会改变BST树的结构，这是无法避免的。但由于我们只关系BST的排列顺序结构，所以内部如何组织和我们毫无关系，不必在意。

5.2 实现

5.2.1 使用引用

void remove(const T &val, BinNode *&cur)
{
    if (cur == nullptr)
    {
        return;
    }
    else if (val < cur->val)
    {
        remove(val, cur->left);
    }
    else if (cur->val < val)
    {
        remove(val, cur->right);
    }
    //对刚好是这个结点的情况进行讨论
    else if (cur->left && cur->right)
    {
        cur->val = findMin(cur->right)->val;
        remove(cur->val, cur->right);
    }
    else 
    {
        BinNode *oldNode = cur;
        cur = (cur->left != nullptr)? cur->left : cur->right;
        delete oldNode;
    }
}

程序十分清楚首先先判断为空，如果 cur 为空或 val 根本不存在，那就会直接 return 回去。

接下来第二三两个 if 判断不断递归找到了需要进行删除的点。然后就来到了第四五两个条件判断块。

如果存在两个子树(这是更加常见的情况，我们把它放到前面)，那么首先现用右子树的最小值来覆盖该结点，然后删除那一个重复的右子树最小值即可。由于右子树的最小值结点不可能有左子树，我们就将第3种情况的问题转化为了第1，2种情况。

就这样，无论是直接到达，还是从第四条判断语句跳转过来，算法最终都会执行到第五条判断，也就是针对最多只有一个孩子的结点进行删除操作。需要注意的是，我们不能直接将结点 delete 就了事，还要对该结点的父节点进行处理，让它指到别处。

好在这里我们的 cur 是一个引用，它等同于 parent->left 或 parent->right，所以直接将它指向 cur 的子树:

如果 cur 无子树，则 parent->* 直接指向 nullptr
如果 cur 有一棵子树，则 parent->* 直接指向该子树

5.2.2 不使用引用

void remove(const T &val)
{
    root = remove(val, root);
}
//返回根节点
BinNode * remove(const T &val, BinNode *cur)
{
    if (cur == nullptr)
    {
        return cur;
    }
    else if (val < cur->val)
    {
        cur->left = remove(val, cur->left);
    }
    else if (cur->val < val)
    {
        cur->right = remove(val, cur->right);
    }
    //对刚好是这个结点的情况进行讨论
    else if (cur->left && cur->right)
    {
        cur->val = findMin(cur->right)->val;
        cur->right = remove(cur->val, cur->right);
    }
    else 
    {
        BinNode *oldNode = cur;
        cur = (cur->left != nullptr)? cur->left : cur->right;
        delete oldNode;
    }
    return cur;
}

5.3 优化

以上程序效率并不高，算法还有优化的空间，主要问题出现在这一段:

1 2	cur->val = findMin(cur->right)->val; cur->right = remove(cur->val, cur->right);

这段程序连续两次对同一个子树进行搜索，这是极大的浪费。解决方法是新定义一个 removeMin() 方法，一次性解决。

void removeMin()
{
    int temp;
    root = removeMin(root, temp);
}
BinNode * removeMin(BinNode *cur, int &minValue)
{
    if (cur == nullptr)
        return nullptr;
    else if (cur->left != nullptr)
        cur->left = removeMin(cur->left, minValue);
    else 
    {
        BinNode *oldNode = cur;
        minValue = oldNode->val;
        cur = (cur->left != nullptr)? cur->left : cur->right;
        delete oldNode;
    }  
    return cur;
}

仅就 removeMin 本身而言，是不需要 minValue 参数的。我们事实上完全可以将cur设为按引用传递然后返回 min 的值。但这里我们没有这么做，而是依旧使用按值传递，是考虑到兼顾很多不支持传递引用的语言。给出更为广泛性适用的算法。

至于 minValue 的引用问题，则没什么大不了。以 Java 为例完全可以自定义一个类，然后将该值取出来——我们可以很简单地定义一个类来替代 int& 的功能，但想代替 BinNode *& 的类就没那么容易定义了。所以相比较之下，我们就选择了这样的编写策略——返回根节点指针，而在参数列表中进行引用传递。

这样一来，remove 方法就可以进一步改进了：

BinNode * remove(const T &val, BinNode *cur)
{
    if (cur == nullptr)
        return cur;
    else if (val < cur->val)
        cur->left = remove(val, cur->left);
    else if (cur->val < val)
        cur->right = remove(val, cur->right);
    //对刚好是这个结点的情况进行讨论
    else if (cur->left && cur->right)
    {
        //改进之后，只查找一次就够了
        cur->right = removeMin(cur->right, cur->val);
    }
    else 
    {
        BinNode *oldNode = cur;
        cur = (cur->left != nullptr)? cur->left : cur->right;
        delete oldNode;
    }
    return cur;
}

6. 其他操作

6.1 清空`makeEmpty`

同之前几个一样，这里清空操作依旧是由一个外部接口来发起一个内部递归的算法。算法的核心思想是：对于一棵树，先清空左子树，再清空右子树，最后把根节点清空。

void makeEmpty()
{
    makeEmpty(root);
}
void makeEmpty(BinNode *&root)
{
    if (root != nullptr)
    {
        makeEmpty(root->left);
        makeEmpty(root->right);
        delete root;
    }
    root = nullptr;
}
~BinarySearchTree()
{
    makeEmpty();
}

有几点要注意的:

最后不要忘了将 root 置为 nullptr 。因为初始时一棵树的根节点就是空。
注意这里我们仍用了指针的引用，主要还是因为根节点。在整棵树清空后，根节点要想有效地置空，必须用引用。否则要加一个返回值才行。

//不用引用的话就要有返回值
void makeEmpty()
{
    root = makeEmpty(root);
}
BinNode * makeEmpty(BinNode *root)
{
    if (root != nullptr)
    {
        root->left = makeEmpty(root->left);
        root->right = makeEmpty(root->right);
        delete root;
    }
    return nullptr;
}

6.2 复制

按照以往惯例，我们同样也写一个 operator=() 然后在拷贝构造函数中直接调用。

BinarySearchTree(const BinarySearchTree &other)
{
    operator=(other);
}

const BinarySearchTree & operator=(const BinarySearchTree &other)
{
    if (this == &other)
        return *this;
    makeEmpty();
    /*???*/
    return *this;
}

仔细想一想，发现拷贝的过程也是一个遍历的过程，还是得用到递归，所以有必要定义另一个 clone 方法用于开启递归算法。

//非常巧妙的构思
BinNode * clone(BinNode *cur)
{
    if (cur == nullptr)
        return;
    return new BinNode(cur->val, clone(cur->left), clone(cur->right));
}

然后在 operator= 中调用:

const BinarySearchTree & operator=(const BinarySearchTree &other)
{
    if (this == &other)
        return *this;
    makeEmpty();
    root = clone(other.root);
    return *this;
}

7. 补充：比较大小操作

之前的操作都是默认 T 重载了 < 的，实际上我们可以通过使用一个 function 对象来优化，使该BST更有泛型特性。

定义一个用于比较的对象

1	function<bool(const T&, const T&)> lessThan;

默认状况下将它赋值为 less<T>()，这时意味着 T 重载了 <
但是要注意，如果是自定义的重载必须为 bool operator <(...) const，尾后的 const 不能省！

1	lessThan = less<T>();

也可以自行定制比较方法

BinarySearchTree(const function<bool(const T&, const T&)> &less = less<T>())
{
    lessThan = less;
    ...
}

使用

struct Point
{
    int x;
    int y;
};

//使用lambda定制操作
BinarySearchTree<Point> l(
    [](const Node &a, const Node &b)->bool
    {
        if (a.x < b.x && a.y < b.y)
            return true;
        else
            return false;
    }
);