1. 引
今天做了一道题:
有一个大西瓜, 用水果刀平整地切, 总共切9刀, 最多能切成多少份, 最少能切成多少份?
最少很好求,就是 10 份呗。关键是最多是多少。
这个问题可以一般化为一个很经典的数学问题:
k 个超平面可以把 n 维空间最多分为多少部分?
我们定义 \(f(n,\ k)\) 表示该问题的解,首先我们会给出这个解的递推公式,然后给出其通项公式。
2. 递推公式
首先考虑平凡问题解:
k 个点可以最多把一条直线分成几个部分?
\(k + 1\) 个1 个超平面可以最多把 n 维空间分成几个部分?
2 个
所以: \[ \begin{cases} f(n,\ 1) = 2\\ f(1,\ k) = k + 1 \end{cases} \]
再考虑一般情况 \(f(n,\ k)\)。我们把它分成两个部分来看:
- 前面 \(k - 1\) 刀把空间分成了几份?
我们不知道,但是我们可以用 \(f(n,\ k - 1)\) 来表示。
- 第 \(k\) 刀给空间多划分了几份?
这个问题就比较关键了。为了方便理解,我们可以从最简单的二维世界开始讲。如果我们已经在平面上划了 \(k - 1\) 条线,现在划第 \(k\) 条线,且需要尽可能多的分割平面应该怎么做呢?
显然,稍加思考就会发现这是一个贪心问题,可以贪心的求解:只需要让新的一条线同之前所有的线都相交就可以了。原本的 \(k - 1\) 条线会把新的线分割成 \(k\) 个部分,然后新增出 \(k\) 个空间出来。
如下图所示,原本三条直线把空间分为 7 个部分,新增了一条线后,一下子多出来了 4 个空间。
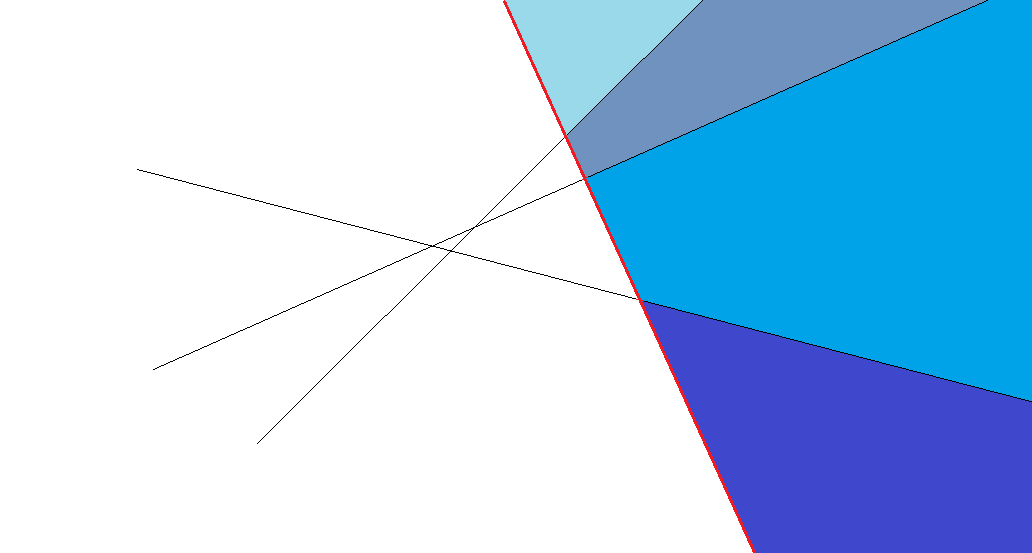
同样的道理扩展到 n 维空间也是一样的。原本已经有了 \(f(n,\ k - 1)\) 个部分,多了一个超平面后,原本的超平面把新的超平面分割为 \(f(n - 1,\ k - 1)\) 个部分,因此也会多处同样数量的子空间出来。
综上所述,我们有:
\[ \begin{cases} f(n,\ 1) = 2\\ f(1,\ k) = k + 1\\ f(n,\ k) = f(n,\ k - 1) + f(n - 1,\ k - 1) & n \geqslant 2 \end{cases} \]
3. 通项公式
通项公式的具体推导很复杂,具体可以见 这里。
这里直接给出结论:
\[ f(n,\ k) = \sum_{i = 0}^{n}\large C_k^i \]
比如在三维空间里,9 个平面最多可以把空间分为:
\[ \large C_9^0 + C_9^1 + C_9^2 + C_9^3 = 130 \]
即 130 个部分。