今天学了一招,是关于 BFS 分批的搜索的,首先看看模型例题。
引例
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如: 给定二叉树 [3,9,20,null,null,15,7],
1 | 3 |
返回其自底向上的层次遍历为:
1 | [ |
倒序倒没什么难度,关键是怎么把每一层分开。最简单的思路是在 BFS 的过程中把深度也存储下来。不过还有一个更好的思路,是一次性搜索完一层,代码如下:
1 | vector<vector<int>> levelOrderBottom(TreeNode* root) |
传统的 BFS 的模板是在每轮的循环中处理队首的结点: 1
2
3
4
5
6
7while (!q.empty())
{
auto n = q.front(); q.pop();
//Do Someting
q.push(n.left);
q.push(n.right);
}
而在这里,我们在每次的循环中直接把当前所有结点出队,处理整个一层的结点。由于在处理过程中,还会有新的结点加入队列,所以我们首先要获知需要处理的结点有几个。
1 | int n = q.size(); |
这个模板的应用会很广泛的。
例子
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1
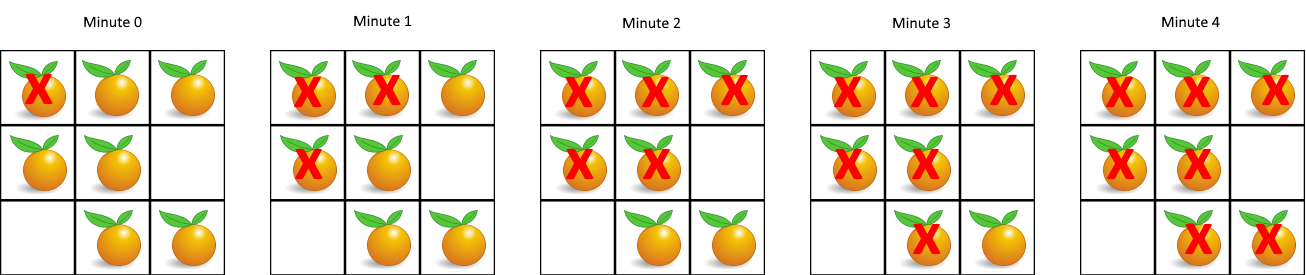
显然,这就是一个一次查找整一层的例子,带入模板,代码如下:
1 | int orangesRotting(vector<vector<int>> &grid) |