第一章 绪论
1. 基本概念
- 数据:信息的载体,能够被计算机识别、存储、加工,包括整数、实数、字符串、图像、声音等
- 数据项:是具有独立含义的最小标识单元,也称字段、域、属性等
- 数据元素:数据的基本单位,也称结点、元素、顶点、记录,一个数据元素可由若干个数据项组成
- 数据对象:性质相同的数据元素的集合
- 数据结构:指数据之间的相互关系,即组织形式。
- 逻辑结构:一般程序中出现的形式
- 线性:如一维数组、栈、队列、链表、串等
- 非线性:如多维数组、广义表、树、图等
- 物理结构:内存中的连续存储形式
2. 算法五个特征
- 输入
- 输出
- 有穷性
- 确定性
- 可行性
第二章 线性表
1. 头指针,头结点,首元结点(第一个元素结点)
头指针是指向链表中第一个结点的指针。
首元结点是指链表中存储第一个数据元素的结点。
头结点是在首元结点之前附设的一个结点,该结点不存储数据元素,其指针域指向首元结点,其作用主要是为了方便对链表的操作。它可以对空表、非空表以及首元结点的操作进行统一处理。
2. 静态链表
使用数组模拟链表
需要额外维护一个空闲链表
3. 习题
填空
- 在顺序表中插入或删除一个元素,需要平均移动 \(\frac{n}{2}\) 和 \(\frac{n-1}{2}\) 个元素,具体移动的元素个数与插入或删除元素的位置有关。
- 顺序表中逻辑上相邻的元素的物理位置一定紧邻。单链表中逻辑上相邻的元素的物理位置不一定紧邻。
- 在单链表中,除了首元结点外,任一结点的存储位置由前驱结点的后继指针指示。
- 在单链表中设置头结点的作用是方便对空表统一处理
在什么情况下用顺序表比链表好?
当所涉及的问题常常进行查找等操作,而插入、删除相对较少时,适合采用顺序表。
判断:顺序表可以存储非线性结构?
对,比如二叉树的数组表示法。
静态链表中指针表示的是
数组下标
第三章 栈和队列
1. 栈的 base 和 top
- 未建立栈时:
base == nulltpr - 空栈:
top == base - 有数据时:
top指向栈顶元素的下一位
2. 出入栈的序列
如果存在入栈序列 i, j, k,则不可能存在出栈序列 k, i, j
3. 中缀式转后缀式算法
- 操作符优先级
(<-=+<*=/<^ - 顺序扫描串,遇到字符就把它放入后缀串或者栈中
- 栈顶元素优先级必须严格大于栈底元素优先级
1 | string convertToPostOrder() |
循环队列(队列的顺序表示法)
- front 和 rear,rear 指向队尾元素的下一个单元
- Enqueue: ++rear
- Dequeue: ++front
- 少用一个单元,若 front 在 rear 的下一个单元,就表示队列满了
1 | bool Empty() const |
第四章 串
1. 空串和空格串的区别
一个是长度为 0 的串,一个是全是空格字符的串
2. 串操作最小子集(一共 5 种)
- StrAssign
- StrCompare
- StrLength
- Concat
- SubString
3. 串的三种表示方式
- 定长顺序存储表示
- 堆分配存储表示
- 块链存储表示
第五章 数组和多维表
1. 多维表的地址计算
对于n维数组:
\[ A_{m_{1}m_{2}\cdots m_{n}} \] 假设主序顺序为从左到右。则: \[ Loc(j_{1}, j_{2},\cdots, j_{n}) = Loc(0, 0, \cdots, 0)+\Big[\sum_{i = 1}^{n-1}\big(j_{i}\prod_{k=i+1}^{n}m_{k}\big)+j_{n}\Big]\times L \]
其中 \(L\) 代表每个单元的存储空间。
例:已知 int a[9][3][5][8],求 a[3][1][2][5] 的地址:
\[ Loc(3, 1, 2, 5) = 0+(3\times(3\times5\times8)+1\times(5\times8)+2\times8+5)\times4 \]
第六章 树与二叉树
1. 树的性质
- 结点数 = 出度 + 1 = 边数 + 1
- 一个 d 次树在第 i 层的结点数 \(\leqslant d^{i - 1}\ (i \geqslant 1)\)
- 高度为 h 的 d 次树结点最多为 \(\frac{d^h - 1}{d - 1}\)
- 树的度是指各个节点度的最大值
2. 二叉树基本概念和性质
- 二叉树是有序树
- 第 i 层至多有 \(2^{i - 1}\) 个结点
- 深度为 k,\(n \leqslant 2^k - 1\)
- n 个结点,深度至少为 \(\lfloor \log_2{n} \rfloor + 1\)
- \(n = n_0 + n_1 + n_2 = n_1 + 2n_2 + 1\)(n = 出度 + 1)
- \(n_0 = n_2 + 1\)
- \(n_0 = \lfloor \frac{n}{2} \rfloor\)
另外有:
- 完全二叉树
- 满二叉树
3. 二叉树的存储
顺序存储结构
适用于完全二叉树
链式存储结构
二叉链表:left, right
有 \(n + 1\) 个空指针域
三叉链表: left, right, parent
有 \(n + 2\) 个空指针域
4. 线索二叉树
- 使用空指针域(一共 n + 1 个)
- 左空指针指向前驱,右空指针指向后继
- 每个结点中增加 LTag 和 RTag 字段用于指明指针到底指向孩子还是前驱后继
- 根据中序、先序和后序可以构造出三种不同的线索
- 先序和后序的线索二叉树遍历时仍然需要父母结点的信息,所以只有中序的线索二叉树常用
5. 树的存储
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
6. 森林与二叉树转换
- 二叉树的左孩子代表原来的树中第一个孩子
- 二叉树的右孩子代表原来的树中的兄弟结点
7. 树的遍历
- 先根遍历:结果等于树转换成二叉树后进行先序遍历
- 后根遍历:结果等于树转换出二叉树后进行中序遍历
- 树没有中序遍历,因为子树无先后之分
第七章 图
1. 图的概念
图分为:
- 无向图
- 有向图:
<v, w>,v->w,v 称为弧尾,w称为弧头
完全图:任意两个点之间都相连
- 无向完全图:\(|E| = \frac{n(n-1)}{2}\)
- 有向完全图:\(|E| = n(n-1)\)
带权图:又称网
度:
- 度 \(TD(v_i)\) = 出度 + 入度 (\(TD(v_i) = OD(v_i) + ID(v_i))\)
- \(|E| = \frac{1}{2}\sum{TD(v_i)}\)
路径:
- 路径、路径的长度、回路
- 简单路径:序列中不出现重复的点的路径
连通性:
- 无向图
- 连通图、连通分量(即极大连通子图)
- 有向图
- 强连通图:任意两个\(v_i\)和\(v_j\),\(v_i \rightarrow v_j\)和\(v_j \rightarrow v_i\)均存在
- 有 \(n\) 个点的强连通图至少有 \(n\) 个弧
- 强连通分量
生成树:
- 是一个极小连通子图
- \(n\) 个点,\(n - 1\) 条边
2. 图的存储
- 邻接矩阵
- 邻接表
- 十字链表
3. 生成树
生成树是一个极小的连通子图,具有图中所有的 n 个顶点,但只有 n - 1 条边。
- 深度优先生成树
- 广度优先生成树
对于带权无向图(网)而言,希望找权值之和最小的生成树,即最小生成树
- Prim 算法
- 反复找到一条连接生成树和其补集的最小分支,把它加入生成树中
- \(O(n^2)\),复杂度只和点有关,和边无关
- 适合边稠密的图
- Kruskal 算法
- 按权值从小到大依次选取分支,并且要求保证不构成回路
- \(O(e\log{e})\),复杂度只和边有关,和点无关
- 适合边稀疏的图
4. DAG 图、AOV 网、拓扑排序
DAG:有向无环图
AOV网:用定点表示活动,用弧表示活动之间的优先关系的有向图
注意,AOV网中不应该出现有向环,判断是否有有向环可以用拓扑排序的方法
拓扑排序:根据偏序关系得到一个全序关系的过程
算法思路:每次从图中找到一个入度为 0 的点,输出;然后把该点和相关的弧从图中删除(相邻的点入度减一);反复循环
算法流程如下:
1 | s = Stack() |
时间复杂度为 \(O(n + e)\)
5. AOE 网、关键路径
6. 最短路径
Dijkstra
复杂度: \(O(n^2)\)
1 | # 额外说明: 用正无穷来表示两个点之间不直接相连,不要使用 0 或其他数字 |
路径打印:将 pathLastNode[start:end] 逆序打印即可
Floyd
思路:
假设一共有 n 个点,则邻接矩阵中有 \(n^2\) 中路径。我们迭代地考察这 n 个点,看是否能通过把当前的被考察点作为中间节点插入到路径中,使得路径变得更短
复杂度: \(O(n^3)\)
1 | # 额外说明: 用正无穷来表示两个点之间不直接相连,不要使用 0 或其他数字 |
打印路径: 1
2
3
4x = i
while x != j:
print(x)
x = path[x][j]
第九章 查找
1. 基本概念
几个基本操作
- 查找某特定数据元素是否在查找表中
- 检索某特定数据元素的各种属性
- 插入
- 删除
- 静态查找表:只有操作 1 和 2
- 动态查找表:操作 1~4 都有
平均查找长度 ASL:
- \(P_i\):记录 i 出现的概率
- \(C_i\):查找记录 i 需要的比较次数
\[ ASL = \sum_{i = 1}^{n}{P_iC_i} \]
2. 静态查找结构
顺序表查找
\[ ASL = \begin{cases} \frac{n+1}{2} &\text{只考虑查找成功的情况}\\ \frac{3(n+1)}{4} & \text{考虑查找失败的情况}\\ \end{cases} \]
折半查找
\[ ASL = \frac{n+1}{n}\log_2{(n+1)} - 1 \]
如果给出了具体的有序表,就得自己画图分析。
分块查找(索引顺序表)
表的数据分块有序(就像快排时候的那样)。
3. 动态查找
BST 二叉搜索树
AVL 平衡二叉树
改进版本的 BST 树。要求任意结点的左右子树高度之差不超过 1。
对每个结点加入一个平衡因子量,用于记录左右子树高度之差。
关于插入时破坏了平衡的处理办法。分为两类四种:
- 单旋(直接向内侧旋转)
- LL
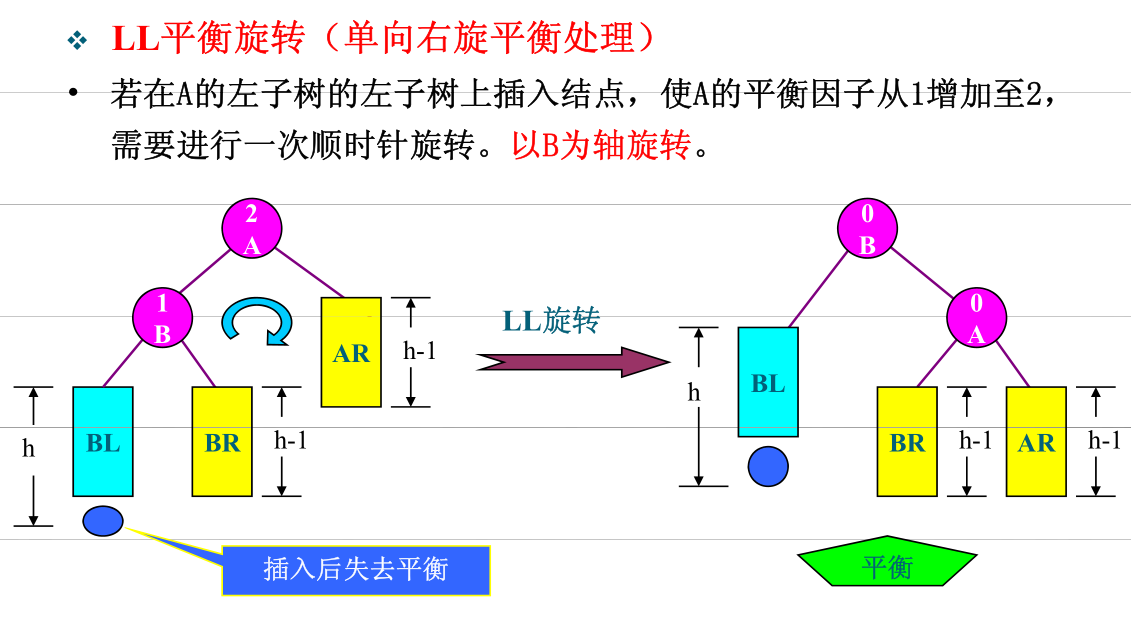
- RR
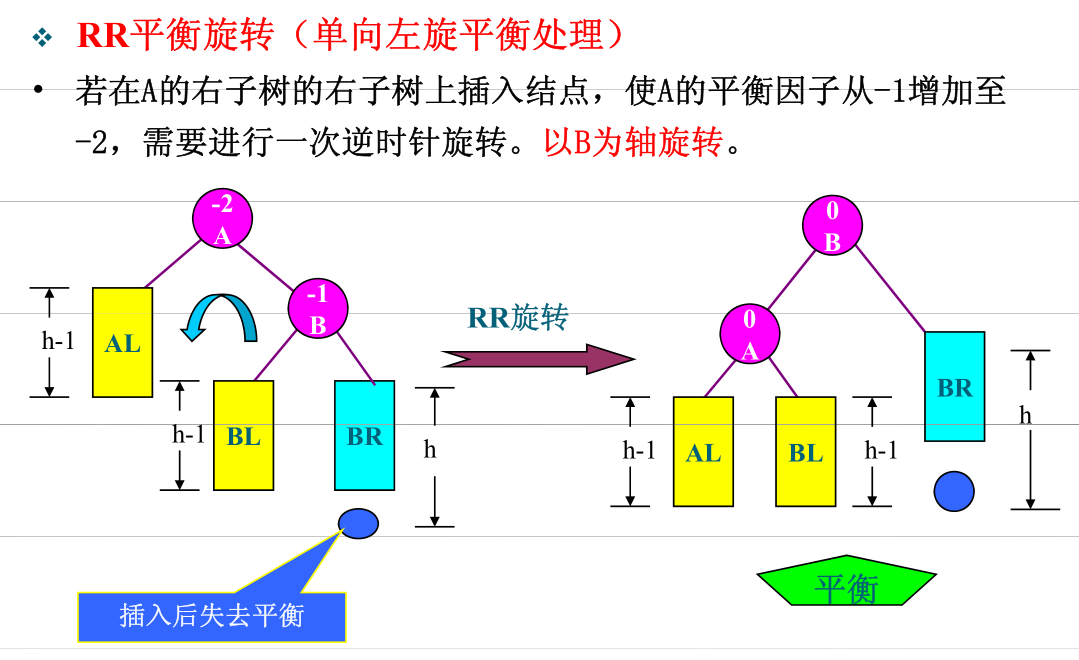
- 双旋(向外后内)
- LR
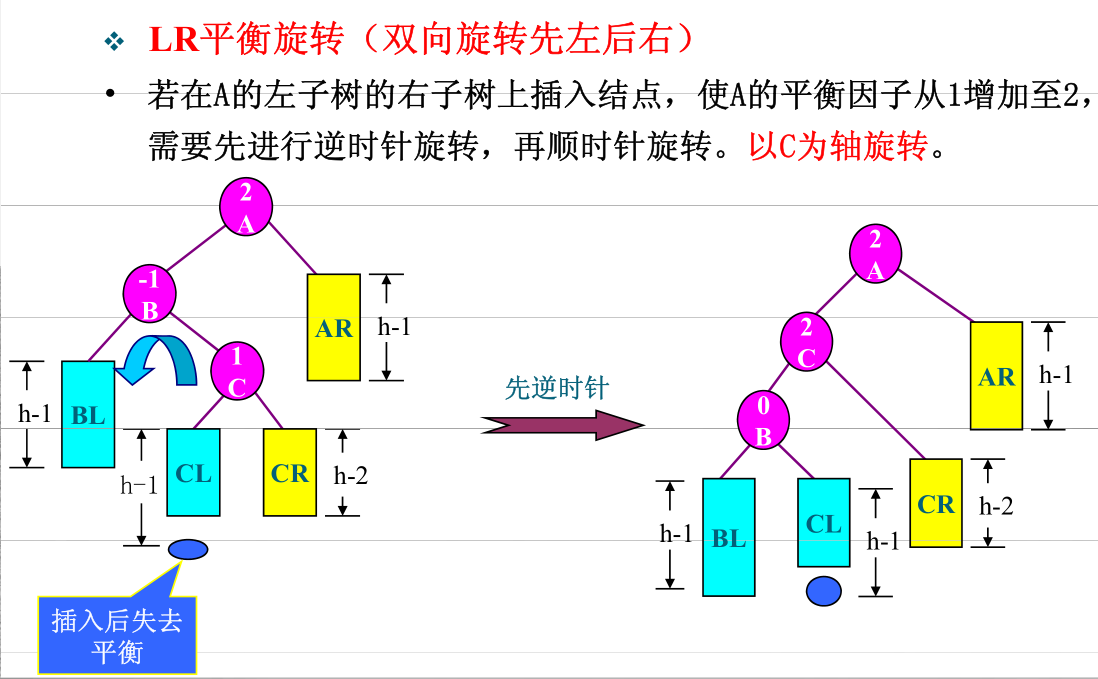
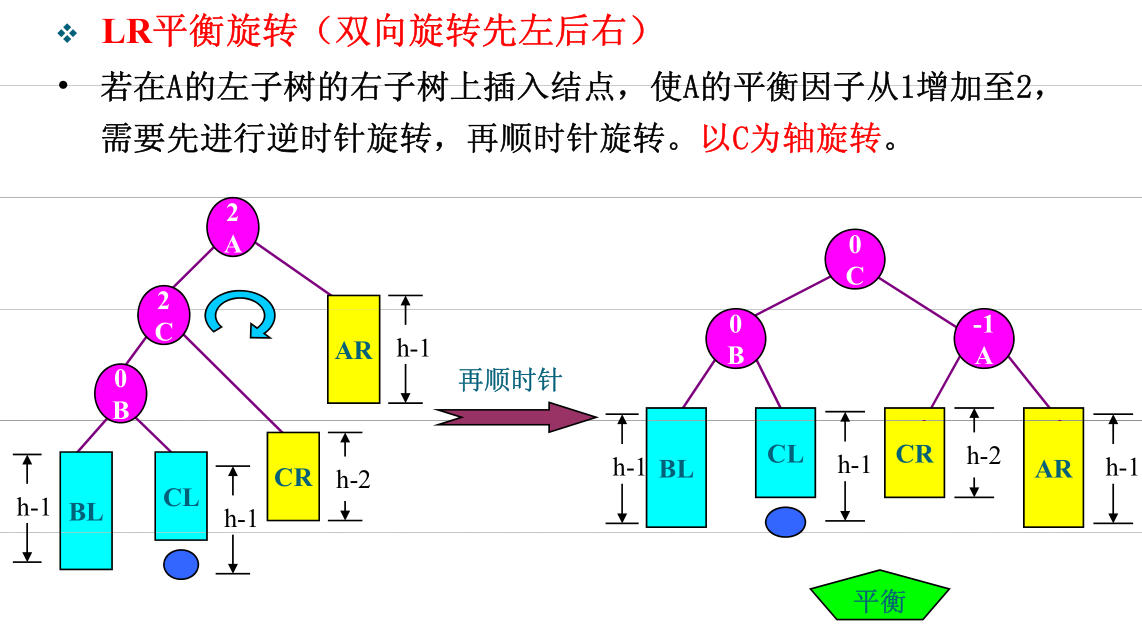
- RL
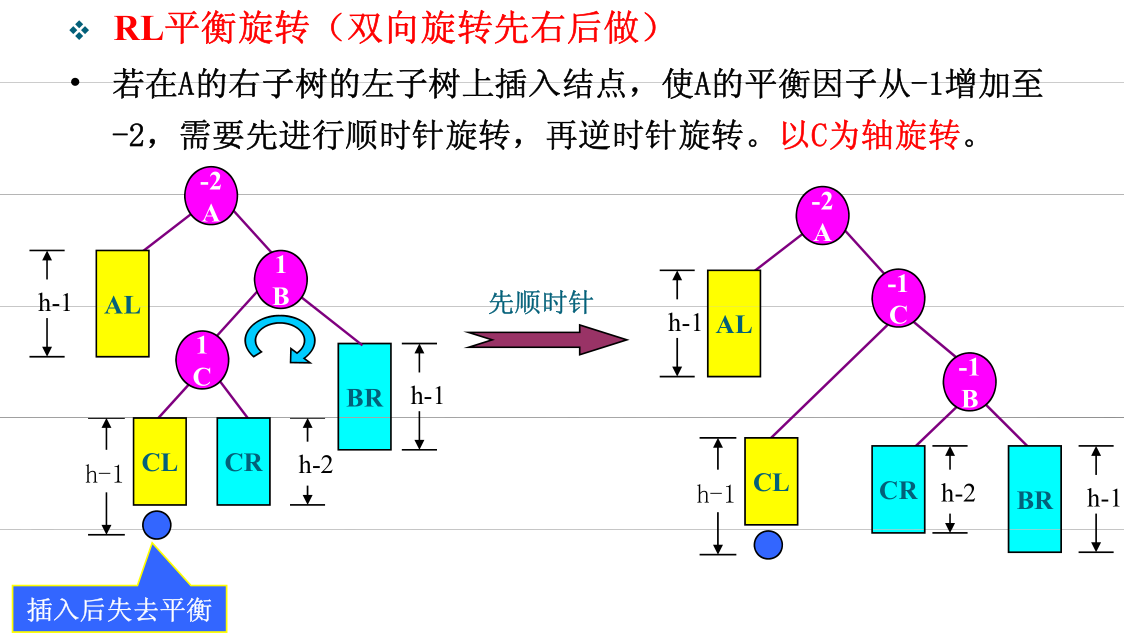
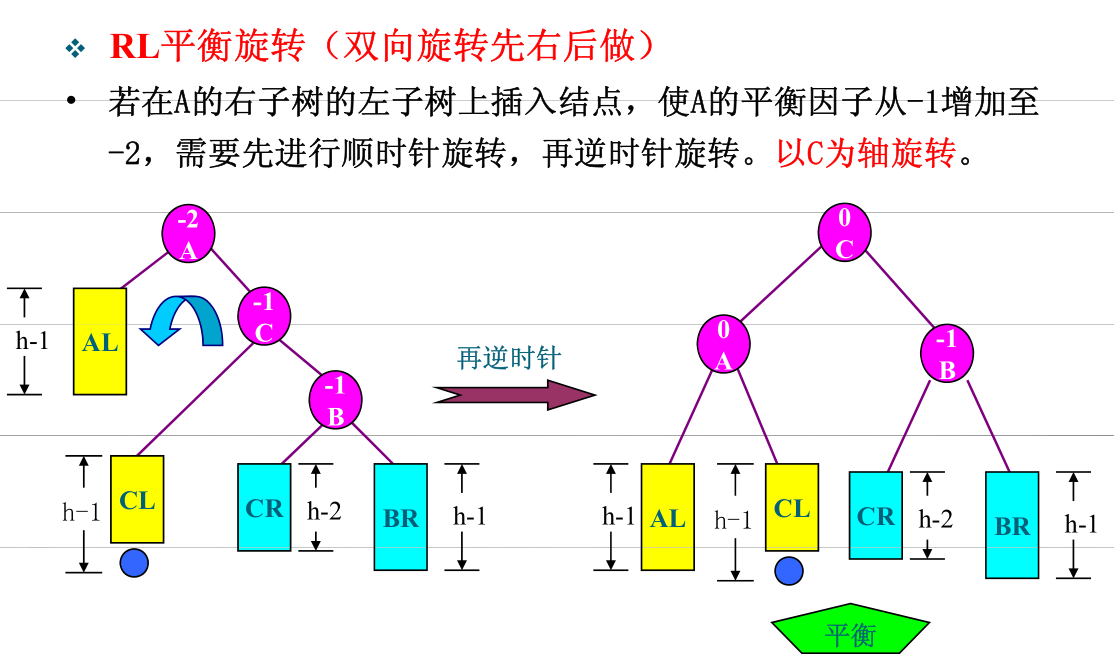
B-树
4. 哈希表
哈希函数构造方法
- 直接定址法
\[ H(key) = a * key + b \]
- 除留余数法
\[ H(key) = key \bmod p,\ key \leqslant m \]
p 一般是一个质数。
处理冲突
- 开放定址法
\[ H_i = (H(key) + d_i) \bmod m \]
\(d_i\) 是一个增量序列。
- 链地址法