本次介绍的三种排序方法,不同于前面所讲的基于比较的方法,其时间复杂度能达到 \(O(n)\) 级别。
1. 计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
1.1 思路
计数排序的思路其实特别简单。对于任意一个数组而言,如果对它的任意一个元素我们能知道小于等于它的元素的个数有多少个,我们就很容易能知道它在排序后应该放在哪个位置。
那么,怎么知道小于等于某个元素的个数呢?很简单,计数就行了。
我们首先需要额外定义一个数组,该数组的下标的范围应当刚好可以覆盖原始数组取值的范围。例如,如果一个数组的取值范围是从 0~20,那么我们就新增加一个长度为 20 的数组,不妨称之为 counter。
接着我们把这一个新增加的数组看作是一个哈希表,counter[i] 就表示 array 中的某个值出现的次数,哪个值呢?最简单的想法当然就是 i 自己了,但很不幸的是,我们还要考虑到 i 有可能是负数,而且还可能出现 array 中的最小值不是 0 的情况。
为了避免这种情况的出现,我们是应该首先求出在原数组当中,最大最小值分别是什么。而哈希函数就取为:
\[ hash(val) = val - minVal \]
1 | for v in array |
接着,我们做一下操作:
1 | for i = [1, rangeLen) |
完成这一步操作之后,counter[i] 就如我们所愿的代表了小于等于 i + minVal 的元素的个数。
完成了以上的操作以后,我们就可以遍历整个数组,找到各个元素对应的计数值,然后放到排序后的数组的对应位置上。
不过还有一个小问题需要我们解决,那就是万一有重复的元素怎么办?
解决的方法是,在最后一步排序的过程当中,我们每处理一个元素 v,就把对应的 counter[v - minVal]--。
比如 counter[5 - 0] == 2。那么我们首先把第一个遇到的元素 5 放在第 2 个位置,然后把 counter[5] 变成 1。这样我们下一次遇到的元素 5 就自动会被放在第 1 个位置了。
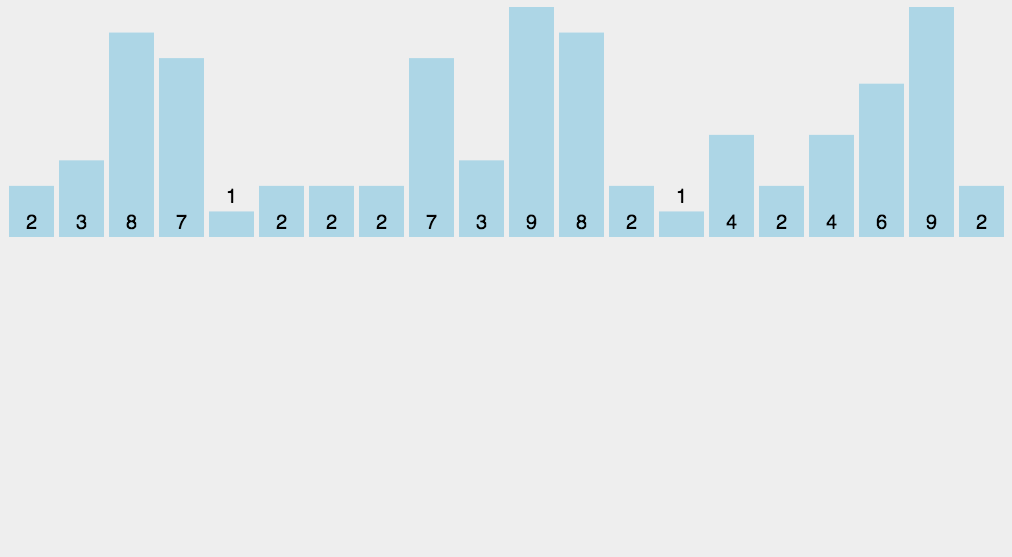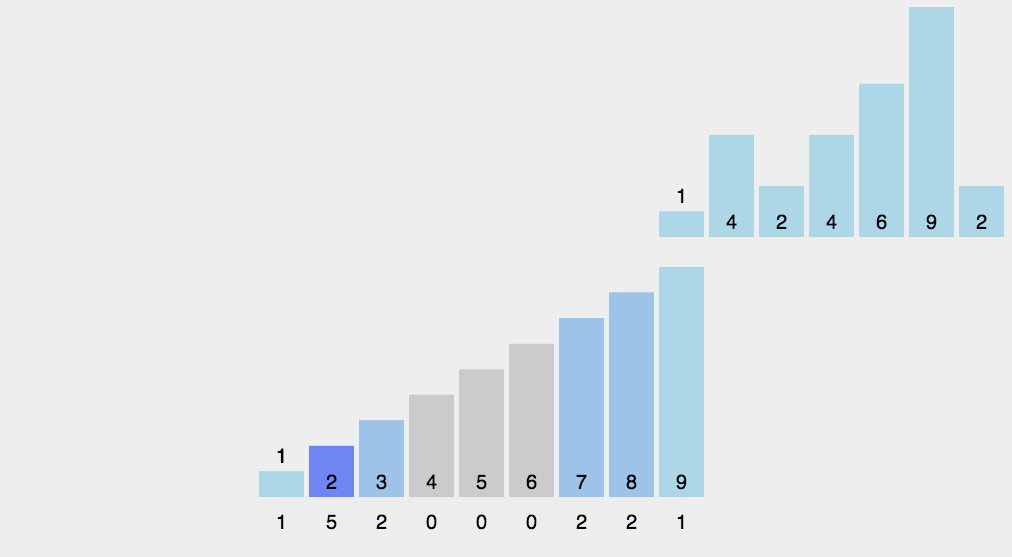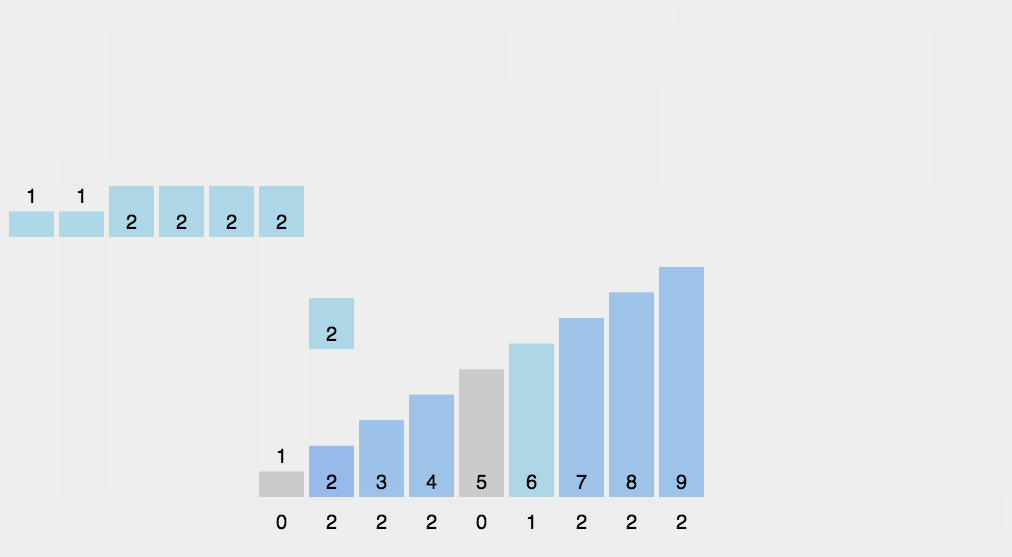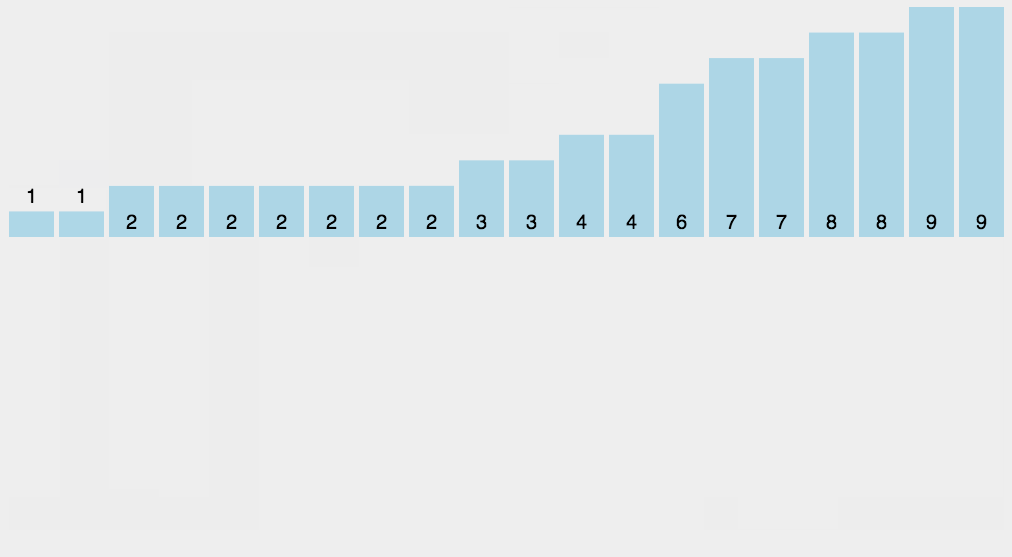
1.2 代码
1 | void CountSort(int *arr, const int len) |
经过上面的解释,这段代码应该不难理解,但是有一个细节点却需要注意一下。
1 | //Attention!!! 从后往前 |
为什么要从后往前呢?其实这涉及到的一个排序的稳定性问题。其实很好懂,这里我们举一个极端的例子。假设有下面这个数组。
1(0) 1(1) 1(2) 1(3) 1(4)
连续五个 1,括号里面是他们的 ID。当我们从前往后放入的时候,首先第一个遇到的元素是 1(0),由于 cnt 为 5,所以我们把它放到了第 5 个位置;然后是 1(1),我们把它放到第 4 个位置,以此类推,最后的排序结果是:
1(4) 1(3) 1(2) 1(1) 1(0)
显然这是一个不稳定的排序,正因如此我们必须从后往前来,让它变成一个稳定的才行。
1.3 分析
- 时间复杂度:\(O(len + rangeLen)\)
- 空间复杂度: \(O(len + rangeLen)\)
- 稳定性:稳定 (前提是必须按照我们之前说明的,从后往前查表)