大整数运算

发表于 | 分类于 ，

1. 引

1.1 简介

最近一段时间刷题的时候，老是遇到大整数高精度运算的题，所以我寻思着要不干脆趁机会把这一类的问题稍微整理一下，以后做题的时候直接套模板上去就行了。

首先来说明一下啥子叫高精度运算。在一般的科学计算中，会经常算到小数点后几百位或者更多，当然也可能是几千亿几百亿的大数字。一般这类数字我们统称为高精度数，高精度算法是用计算机对于超大数据的一种模拟加、减、乘、除、乘方、阶乘、开放等运算。

对于一个很大的数字显然这样的数字无法在计算机中正常存储。于是,我们将这个数字拆成一位一位的或者是四位四位的存储到一个数组中, 用一个数组去表示一个数字。这样这个数字就被称谓是高精度数。

在一般我们做题的时候，涉及到的都是大整数运算，至少我好像还没有看到会涉及到超高精度浮点数运算的题。所以这里我们只整理大整数运算的算法。

那么就实际而言，什么叫大整数呢？这里我整理了一下计算机中常见数据类型的表示范围，如果比这个范围还大，那么就是时候要用到大整数了。

1.2 实际判断大整数的方法

以下各个数据类型最大范围的信息。编译器： gcc version 6.3.0 (MinGW.org GCC-6.3.0-1)。

数据类型 最大值 \(2^n\) 数量级 阶乘范围
int 2147483647 \(2^{31} - 1\) \(2\times 10^9\) (12!, 13!)
long 2147483647 \(2^{31} - 1\) \(2\times 10^9\) (12!, 13!)
long long 9223372036854775807 \(2^{63} - 1\) \(9\times 10^{18}\) (20!, 21!)

也即是说，如果题目当中给出的数据范围小于 \(10^{10}\) 次方或者 \(12!\) 的话，可以使用int。

如果超出了这个数，但是仍然小于 \(10^{18}\) 或者 \(20!\)，我们还可以使用long long来对付一下。

如果比这个还大的话，那就直接用大整数吧。

2. 大整数的构造

2.1 存储

我们之前就说了，可以用一个数组来存储数字的每一位来表示一个大整数。比如这样：

1
short num[200];

既然是用数组来存储数，那就会涉及到两个问题，一个问题是用什么数据类型，另一个问题是数组取多大。

关于第一个问题在这里我使用了 short 类型来存储，因为我们只要用到 0~9 就行了。当然我们还可以用 char 型来表示，这么表示还有一个额外的好处是可以方便输入。

1
scanf("%s", num);

数组的大小，我这里开的是 200，也就是200位。这个数已经非常大了，众所周知，宇宙的直径大约是 920 亿光年，也就是 \(8\times 10^{26}\) 米；宇宙的最小尺度普朗克长度约为 \(1.6\times 10{-34}\) 方米。假如我们把宇宙看成一个三维的立方体，而我们给每个普朗克长度单位的小立方体编个号，总共也不过需要用到 \(10^{183}\) 左右的数字。也就是说现实物理意义上讲，是不可能出现比这个数还大的数的（当然出题人的脑洞是可以超越物理极限）。

2.2 表示

在构造一个大整数的时候，我们应该有两个步骤。

  1. 把整个数组填充为 0
  2. 大部分情况下我们需要构造的整数的各个数位逆序填入数组中

第 1 点比较好理解，因为我们要做加减乘除的时候，肯定需要进位借位，这时候把暂时没有用到的位数设置为 0 是非常合理的。

1
memset(num, 0, sizeof(num));

第 2 点就需要解释一下了，我的意思如图所示：

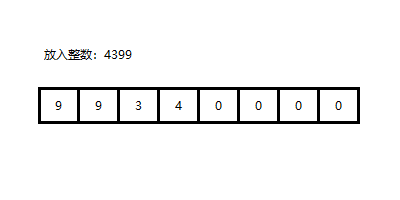
为什么要这么保存呢？这是因为我们所做的大部分运算都是从低位往高位进行的，而且往往会涉及到进位。这时采用逆序保存的方法就会很方便进位操作，反之如果我们按照原始顺序进行保存，想要进位的话，还需要把整个数组往后移动。

当然并不是说，任何情况下都需要用这种顺序来保存。但是在做题的时候，往往只会涉及到加法和乘法，偶尔还有减法，几乎不会涉及到除法。这种情况下采用逆序保存就很合适了。

2.3 包装

现在我们知道，构造一个大整数至少需要一下几个信息：

  • 保存数据的数组
  • 数位长度

所以我们可以构造一个简单的类来保存这些信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Number
{
public:
    //数位长度
    int len = 0;
    //正数
    bool positive = true;
    Number()
    {
        Reset();
    }
    void Reset()
    {
        positive = true;
        memset(num, 0, sizeof(char) * capacity);
    }
    char & operator[](int i)
    {
        return num[i];
    }
    const char & operator[](int i) const
    {
        return num[i];
    }
    friend istream & operator >> (istream &in, Number &n);
    friend ostream &operator <<(ostream &out, const Number &n);
private:
    const static int capacity = 200;
    char num[capacity];
};

num 用于保存数据，长度固定为 200。len 用于保存数位的长度。

另外需要实现 operator[]，之所以要额外实现一个 const 版本的，是因为 operator << 的参数是 const Number &n。而之所以参数要带 const，是为了可以输出临时变量的结果。

最后还要注意一点，我们把是否为正负数的标志单独拿开。这就意味对于一个大整数，我们既可以把它看作一个有符号数也可以看作一个无符号数，所以在后续的算法编写过程当中，总是会有两个版本，一个是无符号型的，一个是有符号型的。

2.4 输入输出

输入的时候，需要记住几点

  1. 判断正负数

如果是负数，我们就把 "-" 替换为 0，然后把数组循环左移一位

  1. 要记得逆序

  2. 对于 '\0'，可以手动把它设为 0，但也可以啥都不做，因为 \0 字符的数值就是 0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
istream & operator >> (istream &in, Number &num)
{
    //重置
    num.Reset();
    cin >> num.num;
    num.len = strlen(num.num);
    //判断负数
    if (num[0] == '-')
    {
        num.positive = false;
        //把 "-" 覆盖掉，然后数组左移
        num[0] = 0;
        rotate(num.num, num.num + 1, num.num + num.capacity);
        //长度减一
        --num.len;
    }
    //逆序, reverse 函数在 <algorithm> 头文件里
    reverse(num.num, num.num + num.len);
    //把 '0'~'9' 搬移到 0~9，不然计算不方便
    for (int i = 0; i < num.len; ++i)
        num[i] -= '0';
    //把最后一个 '\0' 变成 0，这一步可以不做
    num[num.len] = 0;
    return in;
}

注意，输入前一定要重置，否则连续输入的时候就会出现问题。

输出就简单了，反向输出即可。

1
2
3
4
5
6
7
8
ostream &operator <<(ostream &out, const Number &num)
{
    if (!num.positive)
        out << "-";
    for (int i = num.len - 1; i >= 0; --i)
        out << (short)num[i];
    return out;
}

3. 比较

我们分别编写 CmpAbs 和 Cmp 来对有无符号数两种情况进行处理。函数的返回值，遵从C 语言的习惯，即：

  • -1: a < b
  • 0: a = b
  • 1: a > b

3.1 无符号数的比较

当我们把整数看作无符号数时，我们就忽略 positive 标志，只看数位部分。

算法的思路也很简单：

  1. 看两个数的数位长度是否相同
    • 如果不相同就可以直接得出结果
    • 如果相同，跳转到 2 进行比较
  2. 依次从低位到高位进行，数字的大小比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int CmpAbs(const Number &num1, const Number &num2)
{
    int ans = 0;
    //如果长度不同，直接就可以得出结果，否则就逐位比较
    if (num1.len != num2.len)
        ans = num1.len - num2.len;
    else
        for (int i = num1.len - 1; i >= 0; --i)
            if (num1[i] != num2[i])
            {
                ans = num1[i] - num2[i];
                break;
            }
    if (ans < 0)
        ans = -1;
    else if (ans > 0)
        ans = 1;
    else
        ans = 0;
    return ans;
}

3.2 有符号数的比较

这个逻辑很简单，解释略，直接看代码。

1
2
3
4
5
6
7
8
9
10
11
12
int Cmp(const Number &num1, const Number &num2)
{
    int p1 = (int)num1.positive, p2 = (int)num2.positive;
    //若 p1 ^ p2 = 1，则两个数符号不同
    if (p1 ^ p2)
        return p1 - p2;
    //以下是对符号相同情况下的判断
    int ans = CmpAbs(num1, num2);
    if (!num1.positive)
        ans = -ans;
    return ans;
}

4. 加减法

加减法我们放到一块来讲，因为这两个运算之间的关系非常紧密。同样分别按照无符号数的加减法和有符号数的加减法来进行叙述。

4.1 无符号数的加减

4.2.1 加法

大整数的加法应该是最容易实现的，首先要明确一下加法的流程是什么。

从这张图中我们可以看出，其实加法的过程如下：

1
2
3
4
5
6
7
8
9
10
Input: a 位的数 x, b 位的数 y
Output: x + y -> z
竖式对齐 x 和 y，空缺的地方按 0 处理，一共 n 位 (n = max(a, b))
for i = [0, n)
    ci = ai + bi
    if ci > 0
        ci 只保留个位数
        十位数进位到下一位
    endif
endfor

由于在一开始的处理当中，我们把整个数组全部填充为0，所以我们无需对两个数的数位个数不同的情况再做多余处理了。

因此加法的主要关键点就在于实现进位。为此我们可以额外设置一个 carry 变量，该变量记录了上一次相加时的进位，然后在每次做加法的时候，都把 carry 给加入进来。这个思路就有点像硬件电路当中加法器的实现。

1
2
3
4
x = num1[i] + num2[i] + carry;
//进位
carry = x / 10;
ans[i] = x % 10;

代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Number AddAbs(const Number &num1, const Number &num2)
{
    //对齐较大的数位
    int l = num1.len > num2.len ? num1.len : num2.len;
    Number ans;
    //进位
    short carry = 0;
    for (int i = 0; i < l; ++i)
    {
        //相加
        short x = num1[i] + num2[i] + carry;
        //进位
        carry = x / 10;
        ans[i] = x % 10;
    }
    //如果最后还有进位，就增加一个数位
    if (carry != 0)
        ans[l++] = carry;
    ans.len = l;
    return ans;
}

4.2.2 减法

减法的原理和加法是一样的，但是情况要复杂一些。由于减法并非阿贝尔群，所以我们需要分别对 \(a > b\) 和 \(a < b\) 两种情况进行处理。不过幸运的是我们知道 \(a - b = -(b - a)\)，所以如果 \(a < b\)，那么只需把两个参数交换一下，然后加个负号就行了。

下面来看一下减法的过程。

同加法类似减法，也有一个被称为“借位”的机制。我们可以使用类似于在加法中用过的方式，新增加一个 borrowing 变量。

1
2
3
4
t = x[i] - borrowing - y[i];
//不足则继续向高位借位
borrowing = t < 0 ? 1 : 0;
z[i] = t < 0 ? t + 10 : t;

不过在减法当中还有一种特殊的情况需要处理。那就是有可能两个数相减之后，前导部分出现了大量的0。

121 - 120 = 001，先导部分的零不应该被保留

所以在进行完减法处理后，我们需要把前面的零给去掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Number SubAbs(const Number &num1, const Number &num2)
{
    //由于不确定 num1 和 num2 的大小，所以用指针会方便一点.
    const Number *n1 = &num1, *n2 = &num2;
    bool LgSubLs = true;
    //注意，由于是 abs 减法，所以要用 abs 比较
    if (CmpAbs(num1, num2) < 0)
    {
        LgSubLs = false;
        n1 = &num2;
        n2 = &num1;
    }
    //对齐较大的数位
    int l = num1.len > num2.len ? num1.len : num2.len;
    Number ans;
    //借位
    int borrowing = 0;
    for (int i = 0; i < l; ++i)
    {
        //借位相减
        int x = (*n1)[i] - borrowing - (*n2)[i];
        //不足则继续向高位借位
        borrowing = x < 0 ? 1 : 0;
        ans[i] = x < 0 ? x + 10 : x;
    }
    //由于是大减小，所以不会出现循环结束后还有借位
    //但是可能会出现前面后几个0的情况
    //但是要防止把所有 0 都删光了的情况，比如 2 - 2
    //所以要附加 l > 1 的条件
    while (l != 1 && ans[l - 1] == 0)
        --l;
    ans.len = l;
    if (!LgSubLs)
        ans.positive = false;
    return ans;
}

4.2 有符号数的加减

有符号数的加减，其实没什么好说的，就是进行逻辑判断，然后调用无符号数的加减，最后再把正负号的标志给加上去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Number Add(const Number &num1, const Number &num2)
{
    if (num1.positive && !num2.positive)
        return SubAbs(num1, num2);
    else if (!num1.positive && num2.positive)
        return SubAbs(num2, num1);
    Number ans = AddAbs(num1, num2);
    if (!num1.positive)
        ans.positive = false;
    return ans;
}

Number Sub(const Number &num1, const Number &num2)
{
    if (num1.positive && num2.positive)
        return SubAbs(num1, num2);
    else if (!num1.positive && !num2.positive)
        return SubAbs(num2, num1);
    Number ans = AddAbs(num1, num2);
    if (!num1.positive && num2.positive)
        ans.positive = false;
    return ans;
}

5. 乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Number Multiply(const Number &num1, const Number &num2)
{
    Number ans;
    int l1 = num1.len, l2 = num2.len;
    //竖式相乘
    for (int i = 0; i < l1; ++i)
    {
        for (int j = 0; j < l2; ++j)
        {
            //注意是 += 不是 =
            ans[i + j] += num1[i] * num2[j];
            //进位处理
            ans[i + j + 1] += ans[i + j] / 10;
            ans[i + j] %= 10;
        }
    }
    //去除先导的 0, a 位的 x 乘以 b 位的 y，结果的位数不会超过 a + b + 1
    int len = l1 + l2 + 1;
    while (len > 1 && ans[len - 1] == 0)
        --len;
    ans.len = len;
    //确定符号
    short p1 = num1.positive, p2 = num2.positive;
    ans.positive = !(bool)(p1 ^ p2);
    return ans;
}