区间问题

发表于 | 更新于 | 分类于 ，

区间问题是在 OJ 中非常常见的一类贪心算法的问题，这里我做一个总结。

1. 最大不相交覆盖区间问题

1.1 问题描述

在数轴上有 n 个区间 \([a_i, b_i]\)，请从中选取尽可能多的区间，使它们互相之间没有交点(端点不算)

这一类的问题十分常见，在一些活动安排上有很多使用，因而又称会场安排问题。

例题：洛谷的 P1803 凌乱的yyy / 线段覆盖。

题目描述
----------
现在各大oj上有n个比赛，每个比赛的开始、结束的时间点是知道的。
yyy认为，参加越多的比赛，noip就能考的越好（假的）
所以，他想知道他最多能参加几个比赛。
由于yyy是蒟蒻，如果要参加一个比赛必须善始善终，而且不能同时参加2个及以上的比赛。

输入格式
----------
第一行是一个整数n ，接下来n行每行是2个整数ai,bi(ai<bi)，表示比赛开始、结束的时间。

输出格式
----------
一个整数最多参加的比赛数目。

1.2 贪心策略

这种问题的策略很简单：

  1. 将所有区间按照结束点的大小递增排序
  2. 从头到尾遍历，总是贪心地选择更靠前的区间(只要不和已经选择的区间重叠)

1.3 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

struct Cover
{
    int start;
    int end;
};

/**
 * 按照活动的结束时间从小到大排列
*/
bool cmp(Cover &p1, Cover &p2)
{
    return p1.end < p2.end;
}

int main()
{
    int n;
    cin >> n;
    const int len = n;
    Cover lines[len];
    for (int i = 0; i < n; ++i)
        cin >> lines[i].start >> lines[i].end;

    sort(lines, lines + n, cmp);

    //上次参加的比赛的结束时间，参加的比赛数量
    int endTime = INT_MIN, participate = 0;
    for (int i = 0; i < n; ++i)
    {
        //贪心地选择结束时间早的活动参加
        if (endTime <= lines[i].start)
        {
            //参加这次的活动
            ++participate;
            endTime = lines[i].end;
        }
    }
    cout << participate << endl;
    return 0;
}

2. 区间选点问题

2.1 问题描述

数轴上有n个闭区间 \([a_i, b_i]\)。取尽量少的点，使得每个区间内都至少有一个点（不同区间内含的点可以是同一个）

2.2 思路描述

  1. 将所有区间按照结束点的大小递增排序
  2. 选择第一个区间的结束点作为第一个点
  3. 从前往后遍历
    • 如果上一个点在本区间内，就查看下一个区间
    • 否则，选择本区间的结束点作为新的点

2.3 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool cmp(const Interval &a, const Interval &b)
{
    return a.end < b.end;
}


// 排序
sort(vec.begin(), vec.end(), cmp);
//贪心地选择
int pointAt = INT_MIN, pointNum = 0;
for (int i = 0; i < N; ++i)
{
    //若选中的点在当前区间内，就不用管了
    if (pointAt >= vec[i].start && pointAt <= vec[i].end)
        continue;
    else
    {
        pointAt = vec[i].end;
        ++pointNum;
    }
}
cout << pointNum << endl;

实际上，根据我的验证，这类题的代码和最大不相交覆盖问题的代码一模一样。。。只不过为了便于理解写法不同而已。

2.4 例题：POJ 3485 Highway

题目描述

Description
----------
Bob is a skilled engineer. He must design a highway that crosses a region with few villages. Since this region is quite unpopulated, he wants to minimize the number of exits from the highway. He models the highway as a line segment S (starting from zero), the villages as points on a plane, and the exits as points on S. Considering that the highway and the villages position are known, Bob must find the minimum number of exists such that each village location is at most at the distance D from at least one exit. He knows that all village locations are at most at the distance D from S.

Input
----------
The program input is from a text file. Each data set in the file stands for a particular set of a highway and the positions of the villages. The data set starts with the length L (fits an integer) of the highway. Follows the distance D (fits an integer), the number N of villages, and for each village the location (x,y). The program prints the minimum number of exits.
White spaces can occur freely in the input. The input data are correct and terminate with an end of file.

Output
----------
For each set of data the program prints the result to the standard output from the beginning of a line. An input/output sample is in the table below. There is a single data set. The highway length L is 100, the distance D is 50. There are 3 villages having the locations (2, 4), (50, 10), (70, 30). The result for the data set is the minimum number of exits: 1.

Sample Input
----------
100
50
3
2 4
50 10
70 30

Sample Output
----------
1

实际上这道题就是区间选点的一个变型，而且这种变形的方式还挺常见。

题目翻译一下意思是：X轴上公路从0到L，X轴上下有一些点给出坐标代表村庄，问在公路上最少建几个出口才能使每个村庄到出口的距离不超过D。

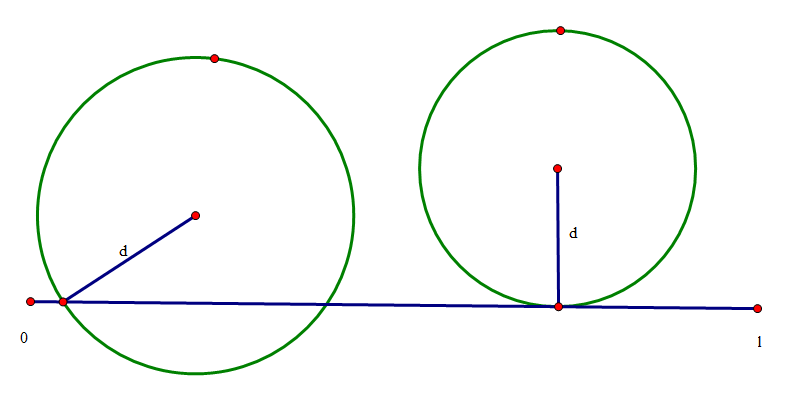
从这张图上看，我们就可以发现，只要计算出每个村庄到公路上的投影，立刻就可以变成区间选点问题。

AC 代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
 * Copyright(c)
 * All rights reserved.
 * Author: Zuo YiPing
 * Date: 2019-07-26-10.50.31
 * OJ Question: POJ 3485 Highways
 * Description: http://poj.org/problem?id=3485
 * Difficulty: 模板题，区间选点问题
 * Key Points: 贪心法
*/
#include <iostream>
#include <vector>
#include <cmath>
#include <climits>
#include <algorithm>
using namespace std;

struct Interval
{
    double start;
    double end;
};

int L, D, N;

bool cmp(const Interval &a, const Interval &b)
{
    return a.end < b.end;
}

int main()
{
    while(cin >> L >> D >> N)
    {
        vector<Interval> vec(N);
        double x, y;
        for (int i = 0; i < N; ++i)
        {
            cin >> x >> y;
            double delta = sqrt(D * D - y * y);
            vec[i].start = x - delta;
            vec[i].end = x + delta;
        }
        sort(vec.begin(), vec.end(), cmp);
        int pointAt = INT_MIN, pointNum = 0;
        for (int i = 0; i < N; ++i)
        {
            //若选中的点在当前区间内，就不用管了
            if (pointAt >= vec[i].start && pointAt <= vec[i].end)
                continue;
            else
            {
                pointAt = vec[i].end;
                ++pointNum;
            }
        }
        cout << pointNum << endl;
    }
    return 0;
}

3. 区间全覆盖问题

3.1 问题描述

数轴上有 n 个闭区间 \([a_i, b_i]\)，选择尽量少的区间覆盖一条指定线段 \([s, t]\)

3.2 思路描述

将所有区间按左端点坐标从小到大排序，顺序处理每个区间。每次选择覆盖点 s 的区间中右端点坐标最大的一个，并将 s更新为该区间的右端点坐标，直到选择的区间已包含 t