堆与二叉堆

发表于 | 更新于 | 分类于 ，

1. 堆的概念

堆又名优先队列，是一种特殊的队列结构(尽管实现可能和队列毫无相似之处)。它的特点如下:

  • 入队: 和正常队列一样把元素插入到数据结构中
  • 出队: 将最小/大的元素出队

根据出队元素是最大的还是最小的元素又可以把堆分类为大顶堆和小顶堆两类。

堆的应用很广泛，最典型的例子就是带有优先级的排队，例如对中断的响应问题：优先响应高优先级的中断，同等优先级的按照顺序排队等。

堆的实现方式有很多，比如可以就用一个列表，然后每次插入的时候按照插入排序的方式来进行，不过这样做很浪费时间，这里我们介绍一种最常见的实现方式——二叉堆。

2. 二叉堆

2.1 概念

二叉堆使用一颗完全二叉树来实现的堆，既然是完全二叉树，那就可以使用一个数组来实现。这里我们从下标 1 开始按照二叉树的结构来填充数组，显然对编号为 x 的结点而言:

  • 它的子结点为 \(2x\) 和 \(2x + 1\)
  • 它的父节点为 \(\lfloor \frac{x}{2} \rfloor\)

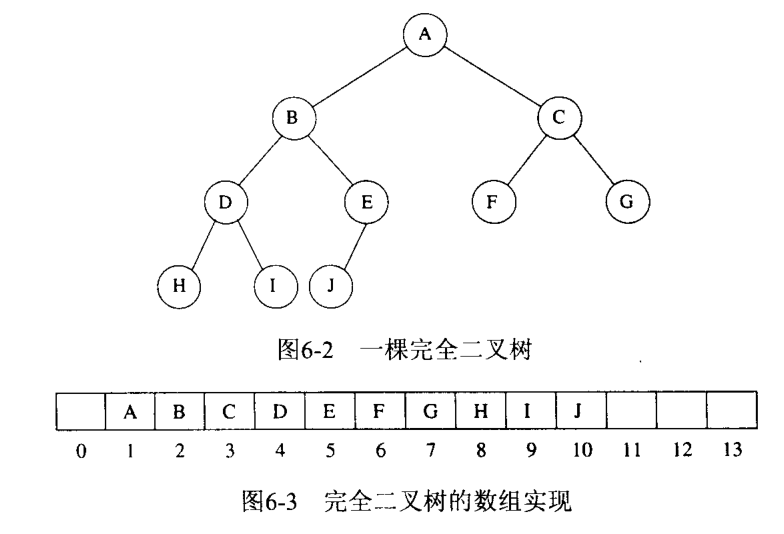
二叉堆有一个重要的性质，在一颗小顶堆中，任意一个结点的值都小于等于其左右子结点的值。若是在大顶堆中则反之。

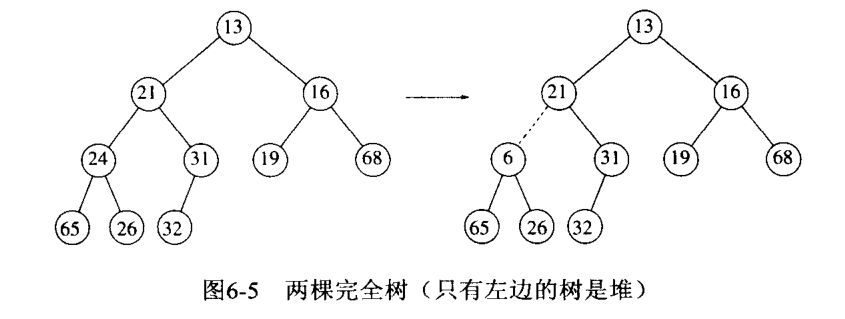
有了这个性质，就最小/大元素总可以在根节点的位置取到。

以下是一颗二叉堆的 ADT:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template<typename Cmp = less<int>>
class Heap
{
public:
    explicit Heap(int capacity = 100);
    void Insert(int val);
    bool Empty();
    int Top();
    void Pop();

private:
    void AdjustTop(int root);
    void CheckIfFull();

    int size;
    vector<int> vec;
    Cmp lessThan;
};

其中利用 Cmp 可以指定比较器，从而来决定是大顶堆还是小顶堆。Insert 用于入队，Pop 可以做出队操作，Top 则是获取队首元素，Empty 用于判断是否为空。

由于是用 vector 来实现，所以额外增加一个 CheckIfFull 用于扩容。

除了出入队操作外，其他几个都很简单，实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
explicit Heap(int capacity = 100)
{
    size = 0;
    vec.reserve(capacity);
}

bool Empty()
{
    return size == 0;
}

int Top()
{
    if (Empty())
        throw 0;
    return vec[1];
}

void CheckIfFull()
{
    if (size + 1 == vec.size())
        vec.resize(vec.size() * 2);
}

2.2 入队操作

插入操作需要小心地维护原本堆的结构，从而保证始终满足堆的性质。一般而言我们的做法如下:

1
2
3
4
5
6
7
8
将新的 value 插入到二叉树最末尾的新结点(空穴)中
Loop
    比较 value 和父节点的值
    if 满足堆的性质
        插入完成, break loop
    else
        交换当前结点和父节点的位置
        goto Loop

整个流程如下:

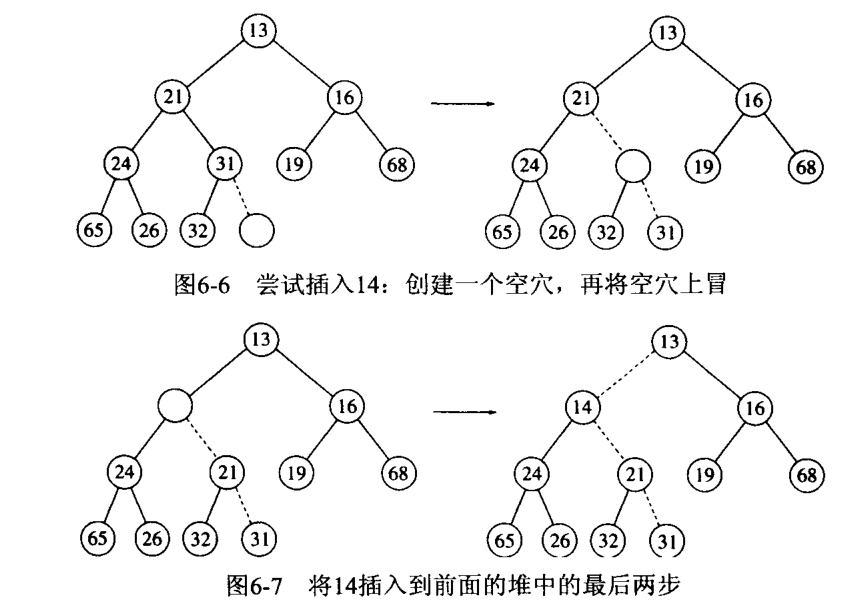
这个过程听起来很复杂，其实很简单，因为仔细一想，这个过程和插入排序的逻辑十分类似，其实都是沿着一个方向有序地插入元素。只不过插入排序里是从前往后，堆的插入里是从叶子节点往根节点方向。

下面是它的实现代码，仔细观察会发现和插入排序的实现很类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * 在堆中插入一个元素，算法有点像插入排序，从末尾出发，找到合适的位置
 * 首先在末尾的空位处插入这个元素，然后不断同父节点比较
 * 如果不满足堆的性质就把父子结点交换，直到满足为止
 * 这样，新的结点就会不断上浮到最佳的位置
*/
void Insert(int val)
{
    //首先检查以下空间够不够，非算法部分
    CheckIfFull();
    int last;
    //从末尾的空穴结点开始，类似插入排序的操作，只不过是在二叉树上进行
    for (last = size + 1; last > 1 && lessThan(val, vec[last / 2]); last /= 2)
        vec[last] = vec[last / 2];
    //找到了合适的位置，插入
    vec[last] = val;
    ++size;
}

2.3 出队操作

出队的操作比较麻烦了，我们需要在删除顶部元素，却又要保证堆的结构合理。这可以看作是这么一个过程:

删除根部结点 -> 找到一个新的根节点满足堆的性质

一个最直白的思路是：从根节点的两个子结点(也可能只有一个)中选一个更小的作为新的根节点。

这是一个好的想法，但存在着一个问题。试想，如果直接把子结点往上移动变成新的根节点，那么原来的子结点的位置就空下来了，所以我们需要递归的对每一个子结点做一个 Pop 操作。

当我们一路向下，不断地把子结点往上提升为父节点时，最终会来到叶子节点。叶子节点是没有子结点，这就意味着必然有叶子结点会变成空结点——而这很有可能会破坏完全二叉树的结构！

所以上面的思路虽然简单但存在很大的问题，问题的根源在于这种算法无法明确最终哪个位置的结点会被删除。而要满足完全二叉树的性质，就必须保证每次都删除最末尾的那个叶子节点。

明确这点，我们知道该怎么做了，很简单:

  1. 删除根节点
  2. 把最末尾的叶子节点移动到根节点的位置作为新的根
  3. 新的二叉树不一定满足二叉堆的性质，需要对二叉树进行调整(AdjustHeap)
  4. 从子结点中选一个更小的和当前父节点交换，然后递归地调整子结点
  5. 当前节点满足堆的性质时，算法结束

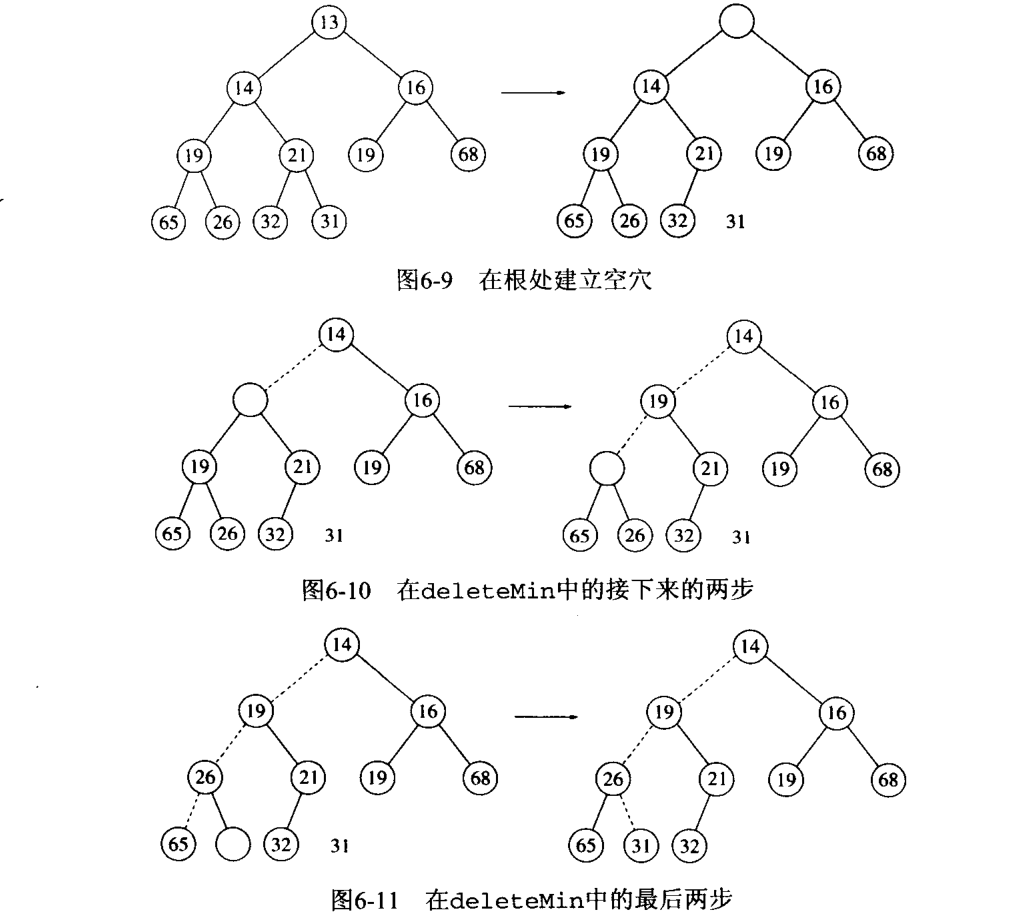
Pop 的代码实现如下:

1
2
3
4
5
6
7
8
9
void Pop()
{
    if (Empty())
        throw 0;
    //末尾结点替代根节点
    vec[1] = vec[size--];
    //调整二叉树
    Adjust(1);
}

Adjust 实现了调整以 root 为根的子树的功能。要求只有 root 的位置不满足堆的性质，其他都满足。算法的实现依旧很像插入排序的逻辑，只不过这次的是从上往下了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * 调整以 root 为根节点的子树，其中 root 不满足堆的性质，需要调整
 * 这个操作依然和插入排序很相似
*/
void Adjust(int root)
{
    //取树根结点的值方便比较
    int rootVal = vec[root];
    //从上到下把根节点下沉
    //循环条件是: root * 2 <= size，即有子树
    //当前根节点调整完毕后，root = child，继续往下调整子树
    for (int child; root * 2 <= size; root = child)
    {
        //左孩子
        child = root * 2;
        //如果有两个子结点，就选它们当中比较小的那一个
        if (child != size && lessThan(vec[child + 1], vec[child]))
            child = child + 1;
        //不满足堆的性质，就用子结点替代父节点
        if (lessThan(vec[child], rootVal))
            vec[root] = vec[child];
        else
            break;
    }
    //找到了合适的位置
    vec[root] = rootVal;
}

2.4 测试

测试小顶堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Heap<> h;
//priority_queue 使用 less 是大顶堆，使用 greater 是小顶堆
priority_queue<int, vector<int>, greater<int>> q;
//priority_queue<int, vector<int>> q;
//插入数据
int n;
while (cin >> n)
{
    if (n == 0)
        break;
    h.Insert(n);
    q.push(n);
}
cout << "优先队列:\n";
while (!q.empty())
{
    n = q.top(); q.pop();
    cout << n << " ";
}
cout << endl;
cout << "堆:\n";
while (!h.Empty())
{
    n = h.Top(); h.Pop();
    cout << n << " ";
}

运行:

2 9 8 7 -12 2 3 -4 2 1 0
优先队列:
-12 -4 1 2 2 2 3 7 8 9
堆:
-12 -4 1 2 2 2 3 7 8 9

测试大顶堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Heap<greater<int>> h;
//priority_queue 使用 less 是大顶堆，使用 greater 是小顶堆
// priority_queue<int, vector<int>, greater<int>> q;
priority_queue<int, vector<int>, less<int>> q;
//插入数据
int n;
while (cin >> n)
{
    if (n == 0)
        break;
    h.Insert(n);
    q.push(n);
}
cout << "优先队列:\n";
while (!q.empty())
{
    n = q.top(); q.pop();
    cout << n << " ";
}
cout << endl;
cout << "堆:\n";
while (!h.Empty())
{
    n = h.Top(); h.Pop();
    cout << n << " ";
}
2 9 8 7 -12 2 3 -4 2 1 0
优先队列:
9 8 7 3 2 2 2 1 -4 -12
堆:
9 8 7 3 2 2 2 1 -4 -12